 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Doua probleme de grupuri
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Prima problema se refera la "slabirea" axiomelor grupului, iar cea de-a doua la compatibilitatea ecuatiei binome într-un grup finit.
Domenii: Grupuri
Soluţie:
I) Fie 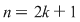 şi fixăm un element şi fixăm un element 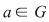 . Cum . Cum 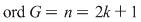 rezultă că rezultă că 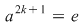 sau sau 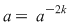 , adică , adică 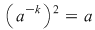 , ceea ce înseamnă că , ceea ce înseamnă că 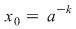 este soluţie a ecuaţiei este soluţie a ecuaţiei 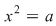 . Dacă . Dacă 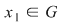 ar fi o altă soluţie a acestei ecuaţii, ţinând cont de faptul că ar fi o altă soluţie a acestei ecuaţii, ţinând cont de faptul că 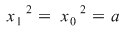 şi că şi că 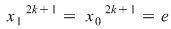 , obţinem: , obţinem: 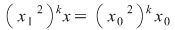 , adică , adică 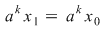 , de unde , de unde 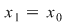 , ceea ce probează unicitatea soluţiei ecuaţiei considerate. , ceea ce probează unicitatea soluţiei ecuaţiei considerate.
II) Putem avea 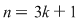 sau sau 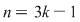 . Dacă . Dacă 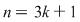 se demonstrează asemănător că unica soluţie a ecuaţiei se demonstrează asemănător că unica soluţie a ecuaţiei 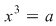 este este 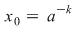 . Dacă . Dacă 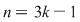 , vom avea că , vom avea că 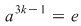 , rezultă , rezultă 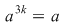 , adică , adică 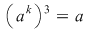 , deci , deci 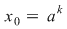 este soluţie a ecuaţiei considerate. Unicitatea se arată ca şi mai înainte. este soluţie a ecuaţiei considerate. Unicitatea se arată ca şi mai înainte.
COMENTARIU
Această problemă admite următoarea generalizare: dacă 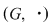 este un grup cu este un grup cu 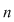 elemente şi elemente şi 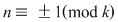 , atunci, pentru orice , atunci, pentru orice 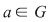 , ecuaţia , ecuaţia 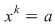 are o soluţie unică în are o soluţie unică în 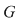 . .
Materiale Didactice Asemanatoare
 Asupra unor probleme de teoria grupurilor Asupra unor probleme de teoria grupurilor
 Structuri algebrice pregrupale Structuri algebrice pregrupale
 Un semigrup remarcabil Un semigrup remarcabil
Bibliografie
| 1. Probleme de structuri algebrice - Nastasescu C., Tena M., Otarasanu I., Andrei Gh. - Editura: Academiei Romane - Bucuresti (anul 1988) |
|