 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
Structuri algebrice pregrupale
În matematica de liceu, prin structură algebrică se înţelege dubletul (sau tripletul) format dintr-o mulţime nevidă şi o lege (sau două legi) de compoziţie, definite pe această mulţime, care verifică un set de proprietăţi numite axiomele structurii respective.
Noţiunea de lege de compoziţie s-a degajat odată cu apariţia grupurilor de substituţii ale lui E. Galois şi a fost cea care a permis lărgirea domeniului de cercetare al algebrei. În acest sens menţionăm algebra Boole, cuaternionii reali descoperiţi de Hamilton şi care au furnizat primul exemplu de corp necomutativ, vectorii, sistemele hipercomplexe şi, mai ales, matricele, descoperite de Cayley, toate acestea făcând ca preocupările algebriştilor să se orienteze, din ce în ce mai mult, către ceea ce se numeşte astăzi structura algebrică abstractă.
D.1. Se numeşte "lege de compoziţie" (sau operaţie algebrică internă) pe mulţimea nevidă 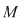 , orice funcţie , orice funcţie 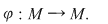
În acest caz, elementul unic determinant 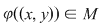 , care este imaginea perechii ordonate , care este imaginea perechii ordonate 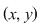 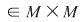 , se notează , se notează 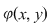 şi se numeşte compusul lui şi se numeşte compusul lui 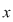 cu cu 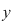 prin legea de compoziţie prin legea de compoziţie 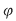 . .
Adesea, în locul lui 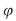 se folosesc alte semne, de exemplu: se folosesc alte semne, de exemplu: 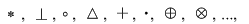 cel mai des cel mai des 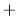 (notaţia aditivă) sau (notaţia aditivă) sau  (notaţia multiplicativă), situaţii în care operaţiile se numesc adunare şi respectiv înmulţire, iar compusele (notaţia multiplicativă), situaţii în care operaţiile se numesc adunare şi respectiv înmulţire, iar compusele 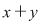 şi şi 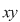 suma şi respectiv produsul lui suma şi respectiv produsul lui 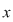 cu cu 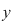 . .
Pentru consideraţiile ce le vom face în continuare, vom nota operaţia algebrică cu 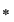 şi vom scrie: şi vom scrie:
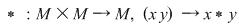 . .
Din multitudinea exemplelor de legi de compoziţie prezentăm:
1. Adunarea şi înmulţirea numerelor întregi:
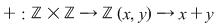

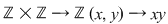
2. Adunarea şi înmulţirea matricelor pătratice de ordinul 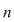 ( (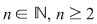 ) cu elemente numere reale: ) cu elemente numere reale:
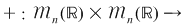
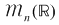 ; ; 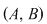 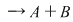
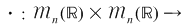
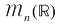 ; ; 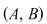 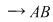
3. Reuniunea şi intersecţia mulţimilor sunt legi de compoziţie pe mulţimea părţilor 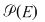 ale mulţimii nevide ale mulţimii nevide 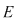 : :
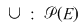
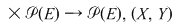 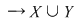
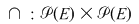
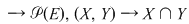
4. Dacă 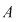 este o mulţime nevidă, iar este o mulţime nevidă, iar 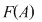 este mulţimea funcţiilor definite pe este mulţimea funcţiilor definite pe 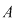 cu valori în cu valori în 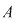 , atunci compunerea funcţiilor este o lege de compoziţie pe mulţimea , atunci compunerea funcţiilor este o lege de compoziţie pe mulţimea 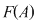 : :
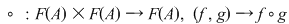 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|