Doua probleme de grupuri
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Prima problema se refera la "slabirea" axiomelor grupului, iar cea de-a doua la compatibilitatea ecuatiei binome într-un grup finit.
Domenii: Grupuri
Două probleme de grupuri
Prima problemă se referă la "slăbirea" axiomelor grupului, iar cea de-a doua la compatibilitatea ecuaţiei 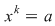 într-un grup finit cu într-un grup finit cu 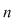 elemente, elemente,
P 1: Fie 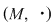 un monoid multiplicativ şi un monoid multiplicativ şi 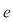 elementul său neutru. Se spune că elementul elementul său neutru. Se spune că elementul 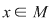 este lateral simetrizabil dacă este simetrizabil la stânga ( este lateral simetrizabil dacă este simetrizabil la stânga (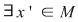 astfel încât astfel încât 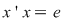 ) sau la dreapta ( ) sau la dreapta (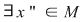 astfel încât astfel încât 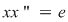 ). ).
Să se demonstreze că următoarele afirmaţii sunt echivalente:
a) 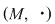 este grup. este grup.
b) Orice element din  este simetrizabil la stânga. este simetrizabil la stânga.
c) Orice element din  este simetrizabil la dreapta. este simetrizabil la dreapta.
d) Orice element din 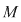 este lateral simetrizabil. este lateral simetrizabil.
e) Orice parte stabilă a lui 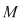 conţine cel puţin un element lateral simetrizabil. conţine cel puţin un element lateral simetrizabil.
Soluţie:
Implicaţia a)  b) este evidenta. b) este evidenta.
b)  c) : c) :
Fie 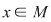 arbitrar. Deoarece arbitrar. Deoarece 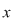 este simetrizabil la stânga, este simetrizabil la stânga, 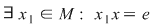 (1) (1)
Cum şi 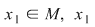 este simetrizabil la stânga, adică este simetrizabil la stânga, adică 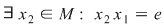 (2) (2)
Înmulţind relaţia (1) la stânga cu 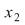 şi ţinând seama de (2) obţinem şi ţinând seama de (2) obţinem 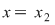 şi atunci relaţia (2) devine şi atunci relaţia (2) devine 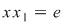 , adică , adică 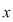 este simetrizabil la dreapta. este simetrizabil la dreapta.
Implicaţiile c) 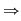 d) şi d) d) şi d) 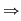 e) sunt evidente. e) sunt evidente.
e) 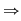 a) : a) :
Dacă 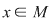 , în partea stabilă , în partea stabilă 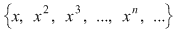 există cel puţin un element lateral simetrizabil, de exemplu există cel puţin un element lateral simetrizabil, de exemplu 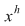 este simetrizabil la stânga. Atunci este simetrizabil la stânga. Atunci 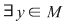 cu cu 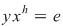 , adică , adică 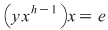 , ceea ce înseamnă că , ceea ce înseamnă că 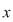 este simetrizabil la stânga. este simetrizabil la stânga.
În concluzie, am demonstrat că orice element 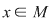 este lateral simetrizabil, adică am stabilit implicaţia e) este lateral simetrizabil, adică am stabilit implicaţia e) 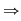 d). d).
Vom arăta, în continuare, implicaţia d) 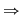 a). Pentru aceasta, luăm a). Pentru aceasta, luăm 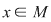 , să zicem simetrizabil la stânga, deci , să zicem simetrizabil la stânga, deci 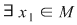 cu cu 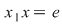 . .
Materiale Didactice Asemanatoare
 Asupra unor probleme de teoria grupurilor Asupra unor probleme de teoria grupurilor
 Structuri algebrice pregrupale Structuri algebrice pregrupale
 Un semigrup remarcabil Un semigrup remarcabil
Bibliografie
| 1. Probleme de structuri algebrice - Nastasescu C., Tena M., Otarasanu I., Andrei Gh. - Editura: Academiei Romane - Bucuresti (anul 1988) |
|