 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
II. Se consideră mulţimea 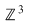 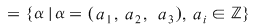 , pe care se defineşte o operaţie algebrică astfel: , pe care se defineşte o operaţie algebrică astfel:
dacă 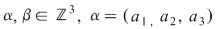 , , 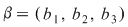 , atunci: , atunci:
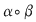 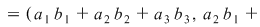
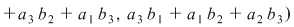
a) Să se studieze asociativitatea şi comutativitatea operaţiei introduse. Admite această operaţie element neutru?
b) Se defineşte o funcţie 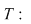 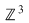 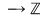 în modul următor: în modul următor:
dacă  , , 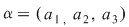 , atunci , atunci 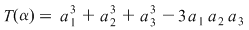 . .
Să se arate că 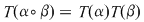 , , 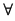 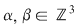 . .
Soluţie:
a) Să considerăm elementele 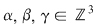 , , 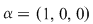 , , 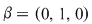 , , 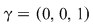 . Avem . Avem 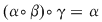 , iar , iar 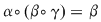 , deci operaţia nu este asociativă. , deci operaţia nu este asociativă.
Apoi 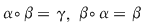 , deci operaţia nu este comutativă. , deci operaţia nu este comutativă.
Să presupunem că există un element neutru 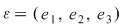 . .
Atunci 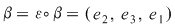 , de unde , de unde 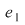 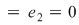 , , 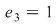 şi de asemenea şi de asemenea 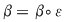 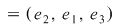 , de unde , de unde 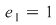 , , 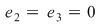 . Egalităţile obţinute sunt contradictorii, ceea ce înseamnă că operaţia nu admite element neutru. . Egalităţile obţinute sunt contradictorii, ceea ce înseamnă că operaţia nu admite element neutru.
b) Se constată tot printr-un simplu calcul că pentru 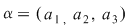 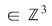 , avem , avem 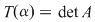 , unde , unde
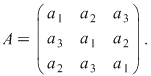 De asemenea, luând şi De asemenea, luând şi 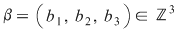 , se constată, efectuând calculele, că , se constată, efectuând calculele, că 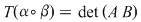 , unde , unde
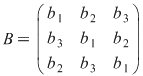
Cum 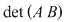 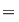 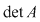 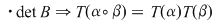 . .
III. Fie 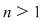 un număr natural. Considerăm mulţimea un număr natural. Considerăm mulţimea 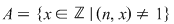 . Să se arate că . Să se arate că 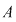 este parte stabilă a mulţimii este parte stabilă a mulţimii 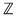 faţă de adunare, dacă şi numai dacă faţă de adunare, dacă şi numai dacă 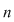 este o putere a unui număr prim. este o putere a unui număr prim.
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|