 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
Soluţie:
Să presupunem că 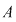 este parte stabilă a lui este parte stabilă a lui 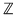 faţă de adunare şi să dovedim că faţă de adunare şi să dovedim că 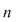 este o putere a unui număr prim. Să presupunem prin absurd că este o putere a unui număr prim. Să presupunem prin absurd că 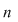 are în descompunerea sa cel puţin doi factori primi distincţi are în descompunerea sa cel puţin doi factori primi distincţi 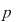 şi şi 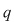 . Atunci există . Atunci există 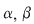 întregi cu proprietatea întregi cu proprietatea
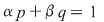 (1) (1)
Deoarece 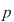 este un divizor comun al numerelor este un divizor comun al numerelor 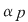 şi şi 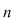 , deducem că , deducem că 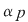  ; analog ; analog 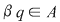 . Egalitatea (1) arată că suma elementelor . Egalitatea (1) arată că suma elementelor 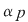 şi şi 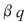 , ambele din mulţimea , ambele din mulţimea 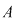 , nu este un element al lui , nu este un element al lui 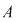 , ceea ce contrazice presupunerea că , ceea ce contrazice presupunerea că 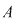 este parte stabilă a lui este parte stabilă a lui 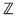 faţă de adunare. faţă de adunare.
Aşadar 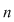 trebuie să aibă un singur factor prim în descompunerea sa, deci este o putere a unui număr prim. trebuie să aibă un singur factor prim în descompunerea sa, deci este o putere a unui număr prim.
Reciproc, să presupunem că 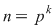 (unde (unde 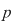 este număr prim, este număr prim, 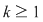 este număr natural) şi să dovedim că este număr natural) şi să dovedim că 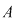 este parte stabilă a lui este parte stabilă a lui 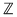 faţă de adunare. Se constată uşor că pentru faţă de adunare. Se constată uşor că pentru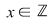 avem echivalenţa avem echivalenţa 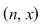 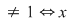 este multiplu de este multiplu de 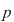 . .
Aşadar 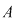 este formată din toţi multiplii întregi ai numărului prim este formată din toţi multiplii întregi ai numărului prim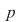 , deci este parte stabilă a lui , deci este parte stabilă a lui 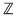 faţă de adunare. faţă de adunare.
IV. Fie 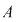 o submulţime a mulţimii numerelor complexe, având proprietăţile: o submulţime a mulţimii numerelor complexe, având proprietăţile:
1. 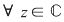 , , 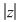 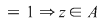
2. 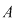 este parte stabilă a lui este parte stabilă a lui 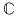 faţă de adunare. faţă de adunare.
Să se demonstreze că 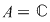 . .
Soluţie:
a) Arătăm mai întâi că discul-unitate este inclus în 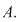
Din proprietatea 1. avem 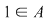 , , 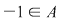 şi atunci şi atunci 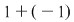 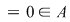 . Fie acum . Fie acum 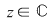 cu cu 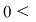 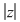 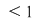 . Considerăm în planul complex punctele . Considerăm în planul complex punctele 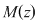 şi şi 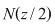 (deci (deci 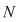 este mijlocul segmentului este mijlocul segmentului 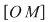 ). Perpendiculara în ). Perpendiculara în 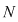 pe pe 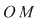 intersectează cercul unitate în punctele intersectează cercul unitate în punctele 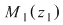 , , 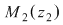 . Deoarece . Deoarece 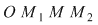 este romb, rezultă este romb, rezultă 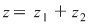 . Cum . Cum 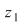 , , 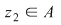 (conform proprietăţii 1.), rezultă (conform proprietăţii 1.), rezultă 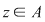 (conform proprietăţii 2.) (conform proprietăţii 2.)
b) Arătăm că şi "coroana circulară" 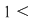 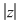 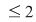 este inclusă în este inclusă în 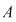 . Fie . Fie 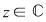 cu cu
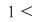
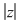 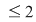 . Considerăm în plan punctele . Considerăm în plan punctele 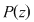 şi şi 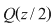 (deci (deci 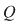 este mijlocul lui este mijlocul lui 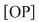 ). ).
Deoarece 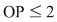 rezultă că rezultă că 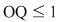 , deci , deci 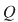 aparţine discului-unitate şi atunci perpendiculara în aparţine discului-unitate şi atunci perpendiculara în 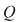 pe pe 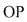 taie cercul unitate în punctele taie cercul unitate în punctele 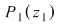 , , 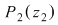 . Rezultă că . Rezultă că 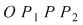 este romb, deci este romb, deci 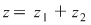 . Dar . Dar 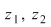  (conform proprietăţii 1.) şi atunci (conform proprietăţii 1.) şi atunci 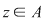 (conform proprietăţii 2.) (conform proprietăţii 2.)
c) Analog (urmează de fapt o inducţie) se arată că şi "coroanele circulare" 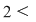 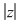 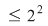 , , 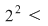 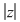 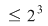 ,..., ,..., 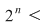 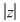 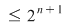 ,... sunt incluse în ,... sunt incluse în 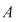 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|