Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
În plus, funcţionează legile puterii:
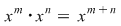 ; ; 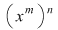 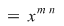 pentru orice element pentru orice element 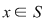 şi orice şi orice 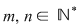 . .
D.13. Grupoidul 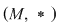 posedă element neutru dacă: posedă element neutru dacă:
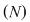 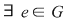 astfel încât astfel încât 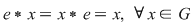 . .
O.14. Observaţii:
(01) Dacă există elementul 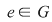 cu proprietatea menţionată se numeşte element neutru (de efect nul) şi el este unic determinat. cu proprietatea menţionată se numeşte element neutru (de efect nul) şi el este unic determinat.
(02) În cazul unui grupoid aditiv, 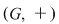 , elementul neutru (dacă există) se notează cu , elementul neutru (dacă există) se notează cu 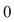 şi se numeşte element zero, iar în cazul unui grupoid multiplicativ, şi se numeşte element zero, iar în cazul unui grupoid multiplicativ, 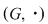 , elementul neutru (dacă există) se numeşte element unitate şi se notează cu , elementul neutru (dacă există) se numeşte element unitate şi se notează cu 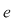 şi nu cu şi nu cu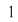 pentru a nu fi confundat cu numărul natural pentru a nu fi confundat cu numărul natural 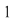 . .
D.15. Un semigrup care posedă element neutru se numeşte monoid (sau semigrup cu unitate).
D.16. Elementul 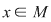 al monoidului al monoidului 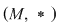 cu elementul neutru cu elementul neutru 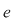 se numeşte simetrizabil dacă: se numeşte simetrizabil dacă:
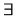 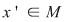 cu cu 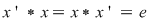 . .
O.17. Observaţii:
(01)Dacă există elementul 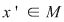 cu proprietatea menţionată, se numeşte simetricul lui cu proprietatea menţionată, se numeşte simetricul lui 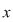 în raport cu operaţia în raport cu operaţia  şi el este unic determinat. şi el este unic determinat.
(02) În cazul unui monoid aditiv, 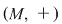 , simetricul lui , simetricul lui 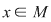 (dacă există) se notează cu (dacă există) se notează cu 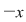 şi se numeşte opusul lui şi se numeşte opusul lui 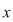 , iar în cazul unui monoid multiplicativ, , iar în cazul unui monoid multiplicativ, 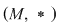 simetricul lui simetricul lui 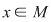 (dacă există), se notează cu (dacă există), se notează cu 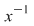 şi se numeşte inversul lui şi se numeşte inversul lui 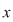 . .
D.18. Dacă 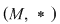 este un monoid cu elementul neutru este un monoid cu elementul neutru 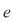 , vom nota mulţimea elementelor sale simetrizabile cu , vom nota mulţimea elementelor sale simetrizabile cu 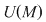 . .
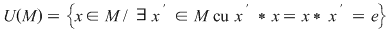 . .
Exemple:
1) 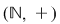 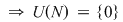
2) 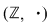 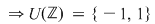
3) 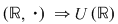 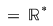
4) 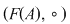 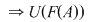 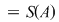
5) 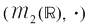 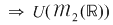 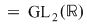 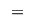
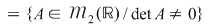
D.19. Un grupoid 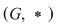 cu proprietatea că fiecare dintre ecuaţiile cu proprietatea că fiecare dintre ecuaţiile 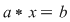 şi şi 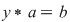 are soluţie unică în are soluţie unică în 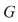 pentru orice pentru orice 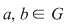 se numeşte quasigrup, iar un quasigrup care posedă element neutru se numeşte buclă (loop). se numeşte quasigrup, iar un quasigrup care posedă element neutru se numeşte buclă (loop).
D.20. Dacă 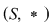 şi şi 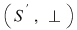 sunt două semigrupuri, funcţia sunt două semigrupuri, funcţia 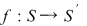 se numeşte morfism de semigrupuri dacă: se numeşte morfism de semigrupuri dacă:
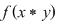 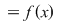 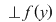 , , 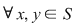 . .
D.21. Dacă 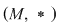 şi şi 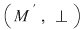 sunt doi monoizi cu elementele neutre sunt doi monoizi cu elementele neutre 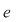 şi respectiv şi respectiv 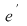 , funcţia , funcţia 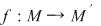 se numeşte morfism de monoizi dacă: se numeşte morfism de monoizi dacă:
1) 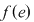 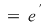
2) 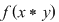 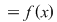 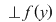 , , 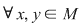 . .
D.22. Un morfism bijectiv de semigrupuri (monopoizi) se numeşte izomorfism.
D.23. Două semigrupuri 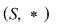 şi şi 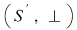 (doi monoizi (doi monoizi 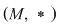 şi şi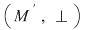 ) se numesc izomorfe dacă între ele există cel puţin un izomorfism. Se scrie: ) se numesc izomorfe dacă între ele există cel puţin un izomorfism. Se scrie:
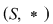 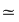 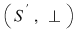 ; ; 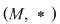 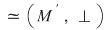
E.24. Exemple:
1) Pentru orice semigrup (monoid) funcţia identică este un morfism de semigrupuri (monoizi). Într-adevăr dacă 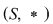 este un semigrup multiplicativ şi este un semigrup multiplicativ şi 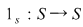 ; ; 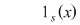 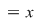 , , 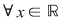 , atunci , atunci 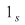 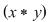 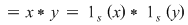 , , 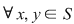 , adică , adică 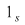 este morfism de semigrupuri. este morfism de semigrupuri.
Dacă 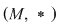 este un monoid cu elementul neutru este un monoid cu elementul neutru 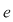 , atunci: , atunci:
a) 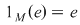
b) 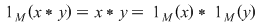 , , 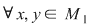 , adică , adică 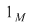 este morfism de monoizi. este morfism de monoizi.
2) Funcţia 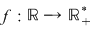 , , 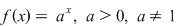 este un izomorfism de monoizi de la este un izomorfism de monoizi de la 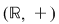 la la 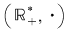 deoarece: deoarece:
1) 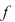 bijectivă bijectivă
2) 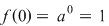
3) 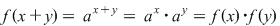 , , 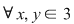
Exerciţii:
I. Dacă 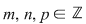 sunt numere întregi fixate şi pe mulţimea numerelor întregi sunt numere întregi fixate şi pe mulţimea numerelor întregi 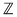 definim operaţia definim operaţia
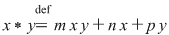 , , 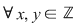 , ,
să se determine:
a) 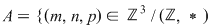 este semigrup este semigrup
b) 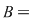 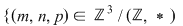 este monoid este monoid
c) Mulţimea elementelor simetrizabile pentru fiecare monoid de la punctul b).
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|