 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
Într-adevăr 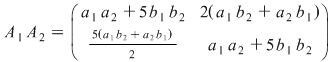 deci deci
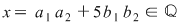 (evident) (evident)
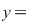
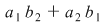 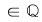 (evident), iar: (evident), iar:
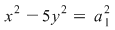
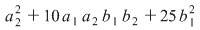
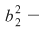
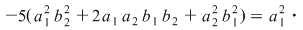
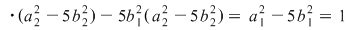
D.8. Operaţia  a grupoidului a grupoidului 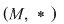 se numeşte: se numeşte:
a) asociativă, dacă: 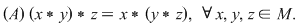
b) comutativă, dacă: 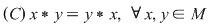 . .
O.9. Observaţii:
(01) Dacă operaţia unui grupoid este asociativă (comutativă), atunci grupoidul respectiv se numeşte asociativ (comutativ).
(02) Tabla unei legi de compoziţie comutativă definită pe o mulţime finită este simetrică faţă de diagonala principală, fiind pefect determinată de partea de deasupra diagonalei principale, inclusiv aceasta.
D.10. Un grupoid asociativ se numeşte semigrup.
D.11. Un semigrup se numeşte semigrup comutativ (abelian) dacă operaţia sa este comutativă.
Exemple:
1. Înmulţirea numerelor întregi determină pe mulţimea numerelor întregi pare: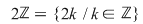 o structură de semigrup abelian. o structură de semigrup abelian.
2. 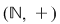 şi şi 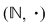 sunt, evident, semigrupuri abeliene. sunt, evident, semigrupuri abeliene.
3. 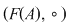 , , 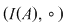 şi şi 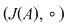 sunt semigrupuri. sunt semigrupuri.
O.12. Observaţii:
(01) Într-un grup, datorită asociativităţii operaţiei sale, este posibilă "suprimarea" parantezelor, menţionând însă ordinea în care se compun elementele.
(02) Într-un semigrup comutativ putem compune un număr finit de elemente în ce ordine dorim.
(03) Există şi grupoizi care NU sunt semigrupuri şi care NU sunt comutativi, de exemplu: 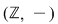 şi şi 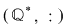 (aici (aici 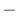 este operaţia de scădere a numerelor întregi, iar este operaţia de scădere a numerelor întregi, iar 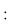 este operaţia de împărţire a numerelor raţionale nenule). este operaţia de împărţire a numerelor raţionale nenule).
(04) Regulile de calcul într-un semigrup 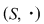 sunt cele datorate asociativităţii legii sale de compoziţie (folosim notaţia multiplicativă pentru comoditatea scrierii) şi anume putem defini (inductiv) puterile cu exponent natural al elementului sunt cele datorate asociativităţii legii sale de compoziţie (folosim notaţia multiplicativă pentru comoditatea scrierii) şi anume putem defini (inductiv) puterile cu exponent natural al elementului 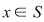 : :
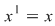 ; ; 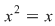 ; ; 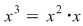 ; ; 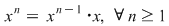 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|