 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
Precizăm faptul că tabla unei legi de compoziţie este extrem de utilă în perfectarea calculelor algebrice şi la verificarea unor proprietăţi ale operaţiei respective.
Din consideraţiile anterioare rezultă imediat:
D.6. Dacă 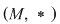 este un grupoid, iar este un grupoid, iar 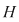 este o submulţime nevidă a lui este o submulţime nevidă a lui 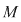 , atunci următoarele afirmaţii sunt echivalente: , atunci următoarele afirmaţii sunt echivalente:
a) 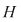 este parte stabilă a lui este parte stabilă a lui 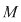 în raport cu legea în raport cu legea 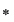 . .
b)  este lege de compoziţie pe este lege de compoziţie pe 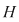 . .
c) 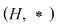 este subgrupoid al grupoidului este subgrupoid al grupoidului 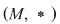 . .
E.7. Exerciţii:
I. Să se arate că mulţimea 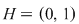 este parte stabilă a lui este parte stabilă a lui  în raport cu operaţia în raport cu operaţia  , unde: , unde:
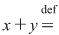 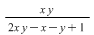 pentru orice pentru orice 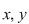 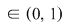
Soluţie: Trebuie arătat că 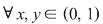 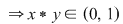 . .
Într-adevăr, dacă 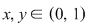 , atunci , atunci 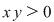 şi şi 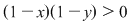 , adică , adică  şi de aici inegalitatea: şi de aici inegalitatea:
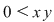
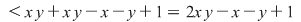 sau sau
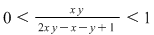 , deci , deci 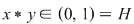 . .
II. Să se arate că, dacă 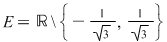 , iar , iar 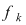 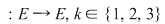 , , 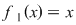 ; ; 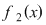 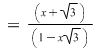 ; ; 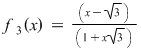 , , 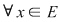 , atunci mulţimea , atunci mulţimea 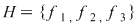 este parte stabilă a lui este parte stabilă a lui 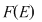 în raport cu operaţia de compunere a funcţiilor. în raport cu operaţia de compunere a funcţiilor.
Soluţie: Într-o astfel de situaţie se alcătuieşte tabla operaţiei induse şi se observă că compusele elementelor din 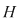 se menţin tot în se menţin tot în 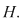
Tabla operaţiei induse pe 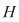 de compunerea funcţiilor din de compunerea funcţiilor din 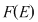 este: este:
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|