 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
D.2. Dubletul 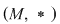 format din mulţimea nevidă format din mulţimea nevidă 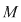 şi legea de compoziţie şi legea de compoziţie 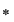 pe pe 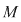 se numeşte grupoid (magmă). se numeşte grupoid (magmă).
În acest caz 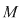 se numeşte mulţimea subiacentă a grupoidului, iar legea de compoziţie se numeşte mulţimea subiacentă a grupoidului, iar legea de compoziţie 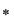 se numeşte operaţia grupoidului. se numeşte operaţia grupoidului.
Din exemplele prezentate deducem că 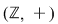 , , 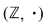 , , 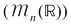 , , 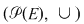 , , 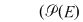 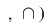 , ,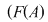 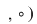 sunt grupoizi. sunt grupoizi.
D.3. Dacă 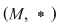 este un grupoid, iar este un grupoid, iar 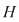 este o submulţime nevidă a lui este o submulţime nevidă a lui 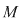 , atunci , atunci 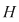 se numeşte parte stabilă (închisă) a lui se numeşte parte stabilă (închisă) a lui 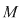 în raport cu operaţia în raport cu operaţia 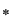 dacă: dacă:
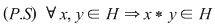 . .
În acest caz se poate defini legea de compoziţie:
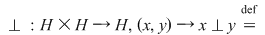
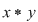 care se denumeşte lege de compoziţie indusă pe care se denumeşte lege de compoziţie indusă pe 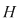 de operaţia de operaţia 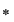 . .
În practică, operaţia 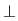 se notează tot cu se notează tot cu 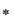 . .
D.4. Dacă 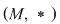 este un grupoid, iar este un grupoid, iar 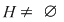 este parte stabilă a lui este parte stabilă a lui 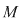 în raport cu în raport cu 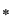 , atunci dubletul , atunci dubletul 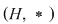 se numeşte subgrupoid (submagmă) a lui se numeşte subgrupoid (submagmă) a lui 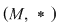 . .
De exemplu, dacă 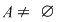 şi şi 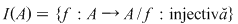 , atunci , atunci 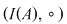 este subgrupoid al grupoidului este subgrupoid al grupoidului 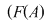 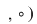 , deoarece compusa a două funcţii injective este tot o funcţie injectivă. În mod analog, dacă , deoarece compusa a două funcţii injective este tot o funcţie injectivă. În mod analog, dacă 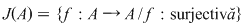 şi şi 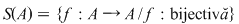 , atunci , atunci 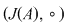 şi şi 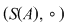 sunt subgrupoizi ai grupoidului sunt subgrupoizi ai grupoidului 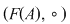 , iar , iar 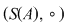 este subgrupoid atât al lui este subgrupoid atât al lui 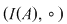 , cât şi al lui , cât şi al lui 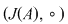 , deoarce orice funcţie bijectivă este atât injectivă cât şi surjectivă. , deoarce orice funcţie bijectivă este atât injectivă cât şi surjectivă.
D.5. Dacă 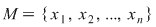 este o mulţime finită, iar este o mulţime finită, iar 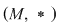 este un grupoid, atunci legea de compoziţie este un grupoid, atunci legea de compoziţie  poate fi dată printr-un tabel cu poate fi dată printr-un tabel cu 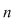 linii şi linii şi 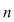 coloane afectate celor coloane afectate celor 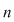 elemente ale mulţimii elemente ale mulţimii 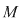 , numit tabla (Cayley) operaţiei , numit tabla (Cayley) operaţiei 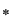 şi care conţine la intersecţia liniei şi care conţine la intersecţia liniei 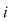 cu coloana cu coloana 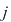 elementul compus: elementul compus: 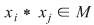 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|