 Optiuni  Inapoi la biblioteca |
Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
V. Fie 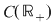 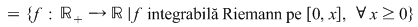 . Pe această mulţime se defineşte operaţia . Pe această mulţime se defineşte operaţia  astfel: astfel:
 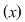 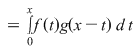 , numită produs de convoluţie. , numită produs de convoluţie.
Să se arate că operaţia este comutativă şi nu are element neutru.
Soluţie:
Făcând schimbarea de variabilă 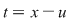 pentru calculul integralei, avem pentru calculul integralei, avem
 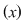 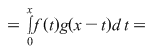
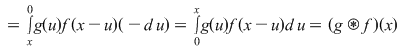 , pentru orice , pentru orice 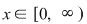 , deci , deci  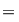  . .
Funcţiile 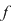 şi şi 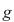 sunt arbitrare în mulţimea sunt arbitrare în mulţimea 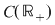 , rezultă că operaţia , rezultă că operaţia  este comutativă. este comutativă.
Să presupunem, prin absurd, că există o funcţie 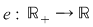 , integrabilă pe orice compact , integrabilă pe orice compact 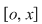 , cu , cu 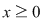 , care este element neutru, adică: , care este element neutru, adică:
 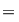  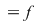 , , 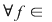 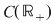 . Luând funcţia . Luând funcţia
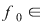 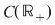 , , 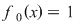 , , 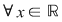 , egalitatea , egalitatea
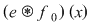 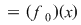 devine: devine:
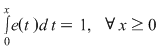 (1) (1)
Făcând 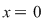 în egalitatea (1), obţinem în egalitatea (1), obţinem 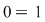 , contradicţie. , contradicţie.
VI. Dacă pe mulţimea 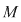 este dată o operaţie algebrică este dată o operaţie algebrică 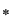 satisfăcând proprietăţile: satisfăcând proprietăţile:
1) Există 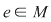 , astfel încât , astfel încât 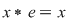 , oricare ar fi , oricare ar fi 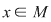 ; ;
2) 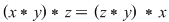 , oricare ar fi , oricare ar fi 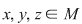 , atunci , atunci 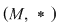 este monoid comutativ. este monoid comutativ.
Soluţie:
Făcând 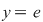 în relaţia 2) şi ţinând seama de 1), obţinem: în relaţia 2) şi ţinând seama de 1), obţinem:
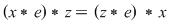 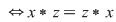 , deci operaţia , deci operaţia 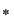 este comutativă. Atunci: este comutativă. Atunci:
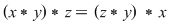
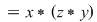 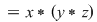 , deci , deci
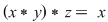 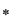 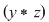 , adică , adică 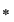 este asociativă. este asociativă.
Rezultă că mulţimea 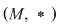 este monoid comutativ. este monoid comutativ.
VII. Pe mulţimea 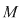 se defineşte o operaţie notată multiplicativ, cu proprietatea se defineşte o operaţie notată multiplicativ, cu proprietatea
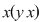 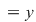 , oricare ar fi , oricare ar fi 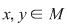 . .
Să se demonstreze că fiecare dintre ecuaţiile 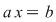 şi şi 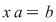 , unde , unde 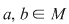 au soluţiue unică în au soluţiue unică în 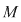 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|