 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Asupra unor probleme de teoria grupurilor
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
În aceasta nota vom prezenta unele rezultate din teoria grupurilor, insistând asupra teoremei lui Lagrange si asupra notiunii de ordin al unui element într-un grup finit, iar apoi vom rezolva 7 probleme de grupuri finite abeliene aplicand aceste doua rezultate. Remarcam faptul ca vom prezenta teorema lui Lagrange evitând notiunile de relatie de echivalenta si multime factor, care sunt incomode pentru o mare parte din elevi.
Domenii: Grupuri
b) Dacă 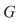 este un grup finit şi este un grup finit şi 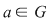 un element arbitrar, atunci există un element arbitrar, atunci există 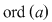 , adică are sens să vorbim de cel mai mic număr , adică are sens să vorbim de cel mai mic număr 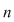 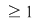 cu cu 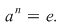
Într-adevăr, cum 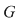 este o mulţime finită, mulţimea este o mulţime finită, mulţimea 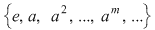 este finită, deci există două numere naturale distincte este finită, deci există două numere naturale distincte 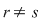 cu cu 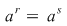 . Dacă presupunem . Dacă presupunem 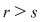 şi notăm şi notăm 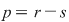 , din egalitatea , din egalitatea 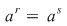 se obţine se obţine 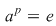 . .
c) Evident, 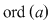 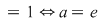 . .
2.1. Să se arate că, dacă 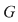 este un grup abelian cu este un grup abelian cu 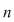 elemente şi elemente şi 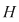 un subgrup propriu al său, astfel încât pentru orice un subgrup propriu al său, astfel încât pentru orice 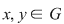 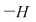 rezultă rezultă 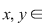 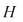 , atunci , atunci 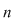 este par şi este par şi
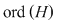 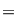 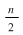 . .
Soluţie : Presupunem că 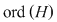 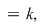 fixăm un element fixăm un element 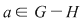 şi considerăm aplicaţia şi considerăm aplicaţia 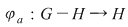 , , 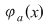 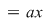 . .
Această aplicaţie este bine definită (în sensul că ia valori în 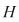 ) datorită ipotezei şi este, evident, injectivă. Rezultă ) datorită ipotezei şi este, evident, injectivă. Rezultă 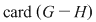 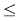 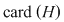 , adică , adică 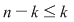 sau sau 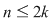 . Pe de altă parte, conform teoremei lui Lagrange, . Pe de altă parte, conform teoremei lui Lagrange, 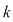 este divizor propriu al lui este divizor propriu al lui 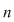 , deci , deci 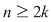 , adică , adică 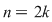 . Prin urmare . Prin urmare 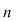 este par şi este par şi 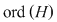 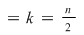 . .
2.2. Să se arate că dacă numărul natural 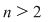 este prim, atunci orice grup cu este prim, atunci orice grup cu 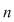 elemente are exact două subgrupuri. elemente are exact două subgrupuri.
Soluţie: Dacă 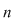 este un număr prim şi este un număr prim şi 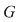 un grup arbitrar cu un grup arbitrar cu 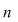 elemente, teorema lui Lagrange ne arată că orice subgrup al acestuia va avea ca ordin un divizor al lui elemente, teorema lui Lagrange ne arată că orice subgrup al acestuia va avea ca ordin un divizor al lui 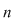 , deci pe , deci pe 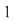 sau pe sau pe 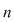 . Prin urmare . Prin urmare 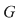 va avea numai două subgrupuri şi anume subgrupurile improprii va avea numai două subgrupuri şi anume subgrupurile improprii 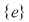 şi şi 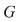 . .
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
Bibliografie
| 1. Probleme de structuri algebrice - Nastasescu C., Tena M., Otarasanu I., Andrei Gh. - Editura: Academiei Romane - Bucuresti (anul 1988) | | 2. Semigrupuri, aplicatii - Nastasescu C., Otarasanu I. - Editura: Militara - Bucuresti (anul 1995) |
|