Polinoame ireductibile, descompunerea in factori ireductibili
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti intr-un corp. Polinoame ireductibile. Descompunerea unui polinom in factori ireductibili: existenta si unicitatea descompunerii. Teorema de caracterizare a polinoamelor ireductibile cu coeficienti in corpul numerelor complexe. . Teorema de caracterizare a polinoamelor ireductibile cu coeficienti in corpul numerelor reale. Aplicatii.
Domenii: Polinoame
6. Polinomul 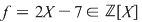 nu are rădăcini în nu are rădăcini în 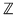 . .
Soluţie: Într-adevăr, dacă pentru 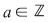 avem avem 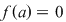 , atunci , atunci 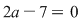 , deci , deci
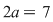 . Dar . Dar 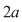 este par şi este par şi 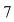 este impar, contradicţie. este impar, contradicţie.
7. Orice polinom 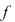 de de 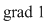 cu coeficienţi dintr-un corp comutativ cu coeficienţi dintr-un corp comutativ 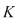 admite o rădăcină în admite o rădăcină în 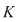 . .
Soluţie: Într-adevăr, fie 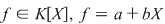 , unde , unde 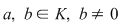 . Fie . Fie 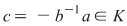 . Atunci, . Atunci, 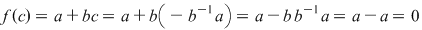 . .
8. Să se găsească rădăcinile polinomului 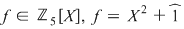 în în 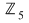 . .
Soluţie: Într-adevăr, funcţia polinomială asociată 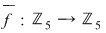 ia valorile date în tabelul: ia valorile date în tabelul:
Deci 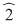 şi şi 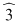 sunt rădăcinile polinomului sunt rădăcinile polinomului 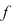 . .
9. Fie 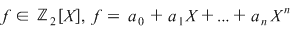 . Arătaţi că . Arătaţi că 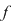 se divide prin se divide prin 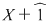 dacă şi numai dacă dacă şi numai dacă 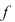 are un număr par de coeficienţi are un număr par de coeficienţi 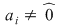 . .
Soluţie: Cum 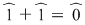 , avem , avem 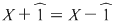 . .
Dar 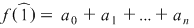 şi cum şi cum 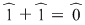 , rezultă că , rezultă că 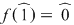 dacă şi numai dacă numărul coeficienţilor dacă şi numai dacă numărul coeficienţilor 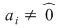 este par. este par.
10. Fie 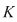 un corp comutativ, un corp comutativ, 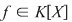 şi şi 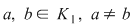 . .
a) Arătaţi că restul împărţirii polinomului 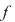 prin prin 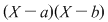 este: este:
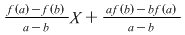
b) Dacă 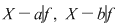 şi şi 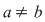 , atunci , atunci 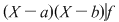 . .
Soluţie:
a) Cum gradul polinomului 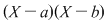 este egal cu este egal cu 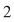 , restul împărţirii lui , restul împărţirii lui 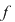 prin prin 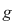 este de forma este de forma 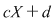 , cu , cu 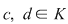 . Fie . Fie 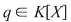 astfel încât astfel încât 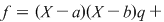
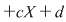 . .
|