 Optiuni  Inapoi la biblioteca  Da un Test Nou Alege nivelul de dificultate:  Moderat Moderat |
Polinoame ireductibile, descompunerea in factori ireductibili
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti intr-un corp. Polinoame ireductibile. Descompunerea unui polinom in factori ireductibili: existenta si unicitatea descompunerii. Teorema de caracterizare a polinoamelor ireductibile cu coeficienti in corpul numerelor complexe. . Teorema de caracterizare a polinoamelor ireductibile cu coeficienti in corpul numerelor reale. Aplicatii.
Domenii: Polinoame
Din prima relaţie avem 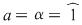 şi şi 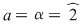 , iar din ultima: , iar din ultima: 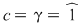 şi şi 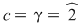 . Deci avem de considerat cazurile: . Deci avem de considerat cazurile:
1) 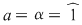 şi şi 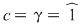
2) 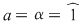 şi şi 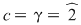
3) 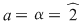 şi şi 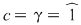
4) 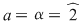 şi şi 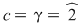
Deoarece 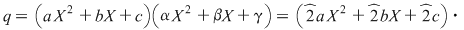
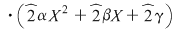 , rezultă că putem considera numai cazurile 1) şi 2). , rezultă că putem considera numai cazurile 1) şi 2).
În cazul 1), înlocuind 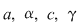 cu cu 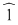 în a doua, a treia şi a patra relaţie, obţinem în a doua, a treia şi a patra relaţie, obţinem 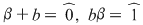 care nu dau valori în care nu dau valori în 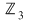 pentru pentru 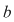 şi şi 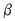 . În cazul 2), înlocuind . În cazul 2), înlocuind 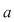 şi şi 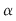 cu cu 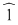 , iar apoi , iar apoi 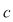 şi şi 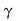 prin prin 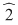 în a doua, a treia şi-a patra relaţie, obţinem în a doua, a treia şi-a patra relaţie, obţinem 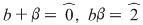 , de unde , de unde 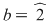 şi şi 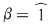 . Deci . Deci 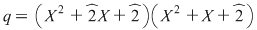 , iar descompunerea în factori ireductibili în , iar descompunerea în factori ireductibili în 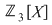 a polinomului a polinomului 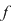 este este 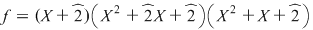 . .
4. Fie 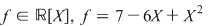 , atunci funcţia polinomială asociată lui , atunci funcţia polinomială asociată lui 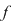 este funcţia reală de o variabilă reală este funcţia reală de o variabilă reală 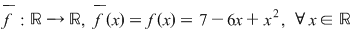 . .
Rădăcinile (din 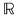 ) ale polinomului ) ale polinomului 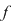 sunt: sunt:
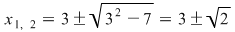 . .
5. Dacă 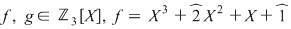 , , 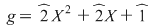 , atunci funcţiile polinomiale asociate , atunci funcţiile polinomiale asociate 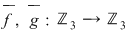 pot fi descrise prin valorile lor în orice pot fi descrise prin valorile lor în orice 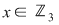 folosind tabelele: folosind tabelele:
Se vede în acest caz că 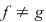 şi totuşi şi totuşi 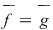 . .
Se observă şi faptul că polinoamele 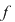 şi şi 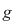 nu au rădăcini în nu au rădăcini în 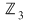 . .
|