 Filtre |
Biblioteca
In cadrul bibliotecii online poti studia 12 articole, 179 lectii.
Articolul zilei: Functii integrabile - Partea II
Funcţii integrabile
(2)
Criterii de integrabilitate.
Cu ajutorul condiţiilor echivalente de integrabilitate se vor putea obţine proprietăţi ale funcţiilor integrabile şi ale integralei, se vor identifica familii de funcţii integrabile.
2.1. Criteriul cu şiruri de sume Riemann.
Teoremă: (criteriul cu siruri de sume Riemann)
Funcţia 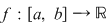 este integrabilă dacă şi numai dacă există un număr real este integrabilă dacă şi numai dacă există un număr real 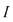 şi pentru orice şir şi pentru orice şir 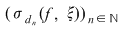 de sume Riemann astfel încât de sume Riemann astfel încât 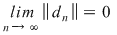 avem avem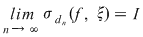 . Atunci . Atunci 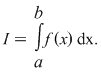
Demonstratie:
Dacă funcţia 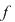 este integrabilă, atunci există un număr real este integrabilă, atunci există un număr real 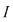 şi pentru orice număr şi pentru orice număr 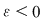 există există 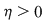 astfel încât pentru orice sumă Riemann astfel încât pentru orice sumă Riemann 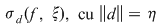 , avem , avem 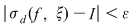 . Atunci, dacă . Atunci, dacă 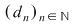 este un şir de diviziuni cu este un şir de diviziuni cu 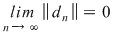 , există , există 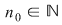 şi pentru orice şi pentru orice 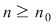 , avem , avem 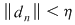 . Rezultă că . Rezultă că 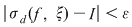 . Recapitulând, pentru orice . Recapitulând, pentru orice 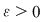 există există 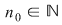 astfel încât pentru orice astfel încât pentru orice 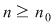 avem avem 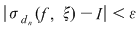 . Aceasta înseamnă . Aceasta înseamnă 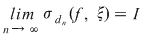 . .
Reciproc, să presupunem că există un număr real 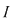 şi că pentru orice şir de sume Riemann şi că pentru orice şir de sume Riemann 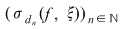 , cu , cu 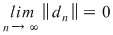 avem avem 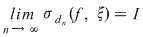 . Să presupunem că funcţia . Să presupunem că funcţia 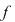 nu este integrabilă. Atunci, pentru numărul nu este integrabilă. Atunci, pentru numărul 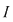 există există 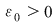 şi, pentru orice număr şi, pentru orice număr 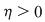 , există o sumă Riemann , există o sumă Riemann 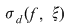 cu cu 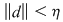 , astfel încât , astfel încât 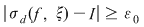 . Alegând . Alegând 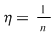 , rezultă că există , rezultă că există 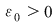 şi pentru orice şi pentru orice 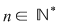 , există , există 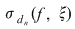 o sumă Riemann cu o sumă Riemann cu 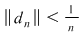 , astfel încât , astfel încât 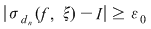 . Atunci şirul . Atunci şirul 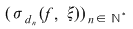 nu converge către nu converge către 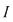 , cu toate că , cu toate că 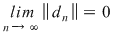 , ceea ce contrazice ipoteza. Funcţia , ceea ce contrazice ipoteza. Funcţia 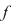 este integrabilă şi este integrabilă şi 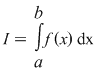 . .
Aplicatii ale monotoniei functiei de gradul al II-lea
Aplicatii ale functiilor de gradul al doilea: determinarea, pentru diferite exemple de functii de gradul al doilea, cu sau fara parametru, a: intervalelor de monotonie, varfului parabolei, intersectiilor cu axele; trasarea graficelor.
Vezi intregul articol | Conjugatul unui numar complex
Definita conjugatului unui numar complex, exemple. Proprietati cu demonstratie: suma, produsul a doua numere conjugate sunt numere reale, conjugatul sumei (produsului, catului) este egal cu suma (respectiv produsul, catul) conjugatelor, un numar complex este egal cu (minus) conjugatul sau daca si numai daca este real (respectiv pur imaginar); aplicatii.
Vezi intregul articol | Formarea ecuatiei de gradul II cand se cunosc radacinile
Formarea ecuatiei de gradul II cand se cunosc radacinile; exemplu.
Vezi intregul articol | Functia exponentiala - definitie si grafic
Functia exponentiala: definitie, exemple cu tabel de valori, convexitate, inegalitatea Jensen, exemple grafice.
Vezi intregul articol |
Materiale didactice
|