 Optiuni  Inapoi la biblioteca  Da un Test Nou Alege nivelul de dificultate:  Moderat Moderat |
Polinoame ireductibile, descompunerea in factori ireductibili
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti intr-un corp. Polinoame ireductibile. Descompunerea unui polinom in factori ireductibili: existenta si unicitatea descompunerii. Teorema de caracterizare a polinoamelor ireductibile cu coeficienti in corpul numerelor complexe. . Teorema de caracterizare a polinoamelor ireductibile cu coeficienti in corpul numerelor reale. Aplicatii.
Domenii: Polinoame
APLICAŢII
1. Să se arate că polinomul 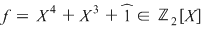 este ireductibil peste este ireductibil peste 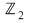 . .
Soluţie: Deoarece 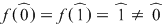 rezultă că rezultă că 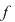 nu are factori de gradul întâi. nu are factori de gradul întâi.
Să arătăm că 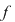 nu se poate scrie ca produs a două polinoame de gradul 2. Într-adevăr, dacă nu se poate scrie ca produs a două polinoame de gradul 2. Într-adevăr, dacă 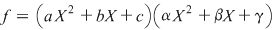 , atunci , atunci 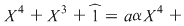
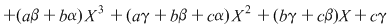 şi egalând coeficienţii obţinem şi egalând coeficienţii obţinem 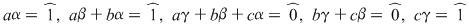 . Din prima şi ultima relaţie, avem . Din prima şi ultima relaţie, avem 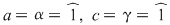 . Înlocuind . Înlocuind 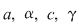 prin prin 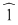 în a doua şi a patra relaţie, obţinem în a doua şi a patra relaţie, obţinem 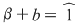 şi şi 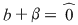 , de unde , de unde 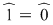 , ceea ce reprezintă o contradicţie. , ceea ce reprezintă o contradicţie.
2. Să se descompună în factori ireductibili peste 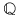 polinomul polinomul 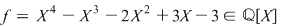 . .
Soluţie: Avem 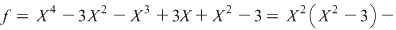
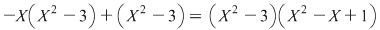 . Este clar că . Este clar că 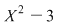 şi şi 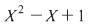 sunt polinoame ireductibile peste sunt polinoame ireductibile peste 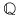 şi deci şi deci 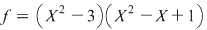 este o descompunere a lui este o descompunere a lui 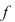 în factori ireductibili în în factori ireductibili în 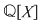 . .
3. Să se descompună în factori ireductibili peste corpul 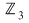 polinomul polinomul 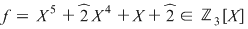 . .
Soluţie: Observăm că 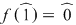 şi deci şi deci 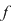 se divide cu se divide cu 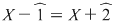 . Folosind schema lui Horner, obţinem câtul împărţirii lui . Folosind schema lui Horner, obţinem câtul împărţirii lui 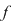 la la 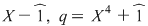 , de unde , de unde 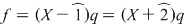 , unde , unde 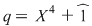 . Deoarece . Deoarece 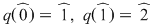 şi şi 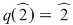 , rezultă că , rezultă că 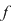 nu mai are alţi factori de gradul întâi. Dacă nu mai are alţi factori de gradul întâi. Dacă 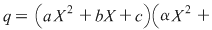
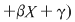 , atunci , atunci 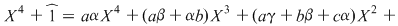
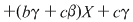 şi prin identificarea coeficienţilor, obţinem şi prin identificarea coeficienţilor, obţinem 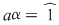 , , 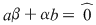 , , 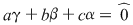 , , 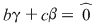 , , 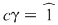 . .
|