Sisteme de ecuatii liniare - cazul general
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XI-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Sisteme de ecuatii liniare: metoda Cramer, descriere; teorema lui Rouche, demonstratie. Exemple.
Domenii: Sisteme liniare
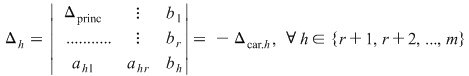
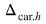 reprezintă minorul caracteristic ecuaţiei secundare reprezintă minorul caracteristic ecuaţiei secundare 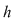 , care este un minor de ordin , care este un minor de ordin 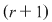 ce se obţine prin "bordarea" minorului principal cu o linie formată din coeficienţii necunoscutelor principale din ecuaţia secundară ce se obţine prin "bordarea" minorului principal cu o linie formată din coeficienţii necunoscutelor principale din ecuaţia secundară 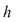 şi o coloană formată din termenii liberi ai ecuaţiilor principale şi ecuaţiei secundare şi o coloană formată din termenii liberi ai ecuaţiilor principale şi ecuaţiei secundare 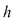 . .
Prin urmare: 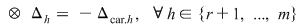 . Folosind acest rezultat putem studia compatibilitatea lui . Folosind acest rezultat putem studia compatibilitatea lui 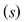 . .
1) Dacă 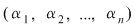 este o soluţie a lui este o soluţie a lui 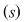 atunci: atunci:
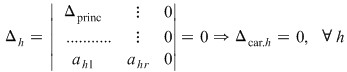
2) Dacă 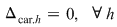 şi şi 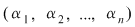 este o soluţie a lui este o soluţie a lui 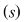 , atunci folosind , atunci folosind 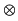 găsim: găsim:
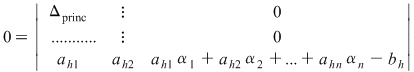 , adică , adică 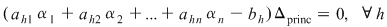 şi cum şi cum 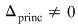 , rezultă că , rezultă că 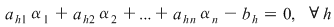 , adică soluţia lui , adică soluţia lui 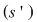 verifică şi ecuaţiile secundare, deci este soluţie a lui verifică şi ecuaţiile secundare, deci este soluţie a lui 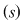 . .
Am demonstrat, astfel, teorema lui Rouche:
Un sistem de ecuaţii liniare de rang strict mai mic decât numărul ecuaţiilor este compatibil dacă şi numai dacă toţi minorii caracteristici sunt nuli. Dacă un minor caracteristic este nenul, atunci sistemul este incompatibil.
Practic, se urmează următorul algoritm:
1) Se determină 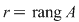 şi se precizează şi se precizează 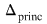 , ecuaţiile principale - ecuaţiile secundare, necunoscutele principale - necunoscutele secundare. , ecuaţiile principale - ecuaţiile secundare, necunoscutele principale - necunoscutele secundare.
2) 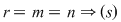 compatibil determinat cu soluţia compatibil determinat cu soluţia 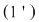 . .
3) 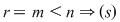 compatibil nedeterminat cu soluţia compatibil nedeterminat cu soluţia 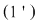 . .
4) 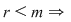 se calculează toţi cei se calculează toţi cei 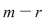 minori caracteristici: minori caracteristici:
* toţi 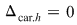 , atunci , atunci 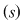 compatibil compatibil 
* există un 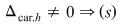 incompatibil. incompatibil.
Pentru sistemele omogene 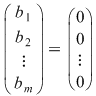 facem precizările: facem precizările:
|