 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Sisteme de ecuatii in Zn
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Inelul claselor de resturi : definitie, unitati. Sisteme de ecuatii liniare cu coeficienti in inelul claselor de resturi, exemple. Mica teorema a lui Fermat, exemple.
Domenii: Inele
Observaţie :
Este necesar să precizăm această bine definire deoarece există numere întregi diferite care au clase egale (de exemplu: 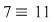 (mod 4)) (mod 4))
Operaţiile astfel definite induc pe mulţimea 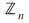 o structură algebrică de inel (unitar şi comutativ), numit inelul claselor de resturi modulo o structură algebrică de inel (unitar şi comutativ), numit inelul claselor de resturi modulo 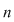 . .
Axiomele inelului 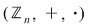 se verifică cu uşurinţă. Precizăm că elementul neutru al grupului se verifică cu uşurinţă. Precizăm că elementul neutru al grupului 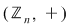 este este 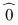 , iar opusa unei clase , iar opusa unei clase 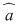 în acest grup este: în acest grup este: 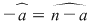 . De asemenea, elementul unitate al monoidului . De asemenea, elementul unitate al monoidului 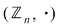 este este 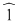 şi o clasă şi o clasă 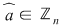 se numeşte inversabilă dacă este inversabilă în monoidul se numeşte inversabilă dacă este inversabilă în monoidul 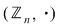 , adică există , adică există 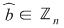 cu cu 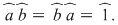
Dacă o astfel de clasă 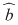 există, atunci ea este unică, se numeşte inversa lui există, atunci ea este unică, se numeşte inversa lui 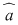 şi se notează şi se notează 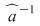 . .
Mulţimea elementelor inversabile ale inelului 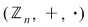 se notează cu se notează cu 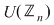 (unităţile lui (unităţile lui 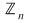 ) şi are loc urmatoarea: ) şi are loc urmatoarea:
Propoziţie :
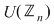
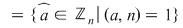
Demonstraţie :
"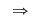 " Fie " Fie 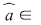 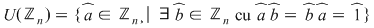
Dacă 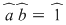 atunci atunci 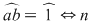 divide divide 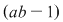
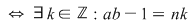 sau sau 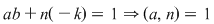
(Am folosit un cunoscut rezultat din aritmetica numerelor întregi : 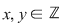 cu cu
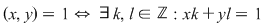 ) )
" 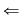 " Dacă " Dacă 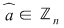 şi şi 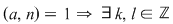 cu cu 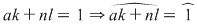
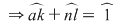
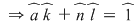 şi cum şi cum 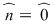 obţinem că obţinem că 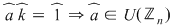
De exemplu :
1) 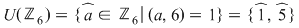 şi şi 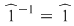 (deoarece (deoarece 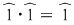 ) )
 (deoarece (deoarece 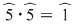 ) )
2) 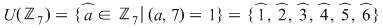
şi 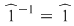 ; ; 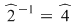 ; ; 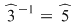 ; ; 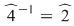 ; ; 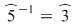 ; ; 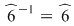
De aici extragem un rezultat foarte important pentru partea a doua a acestui articol.
 Dacă Dacă 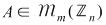 atunci atunci 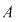 este inversabilă dacă şi numai dacă este inversabilă dacă şi numai dacă 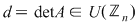 . .
În această situaţie: 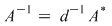
Bibliografie
| 1. Structuri algebrice fundamentale - Otarasanu I. - Editura: Junior - Bucuresti (anul 2000) | | 2. Bac 2003 - Borcea C., Cavachi C., Enescu A., Otarasanu I., Schiopu D. - Editura: Ager (anul 2003) | | 3. Sisteme de ecuatii liniare - Ganga M. - Editura: Mathpress (anul 1996) |
|