 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Sisteme de ecuatii in Zn
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Inelul claselor de resturi : definitie, unitati. Sisteme de ecuatii liniare cu coeficienti in inelul claselor de resturi, exemple. Mica teorema a lui Fermat, exemple.
Domenii: Inele
 SISTEME DE ECUAŢII ÎN SISTEME DE ECUAŢII ÎN 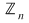
În prima parte a acestei note vom construi (în mod elementar) inelul claselor de resturi modulo 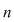 şi vom determina grupul unităţilor (elementelor inversabile) acestui incel, iar în partea a doua vom indica metodele de rezolvare a unui sistem de ecuaţii liniare (pătrat) cu coeficienţi în şi vom determina grupul unităţilor (elementelor inversabile) acestui incel, iar în partea a doua vom indica metodele de rezolvare a unui sistem de ecuaţii liniare (pătrat) cu coeficienţi în 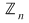 şi vom rezolva câteva astfel de sisteme. În final vom face câteva observaţii. şi vom rezolva câteva astfel de sisteme. În final vom face câteva observaţii.
 I. Inelul claselor de resturi modulo
I. Inelul claselor de resturi modulo 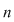
Dacă 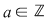 şi şi 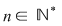 , teorema împărţirii cu rest a lui , teorema împărţirii cu rest a lui 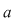 la la 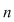 spune că există spune că există 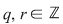 , unice, astfel încât : , unice, astfel încât : 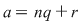 şi şi 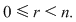
Cum 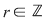 şi şi 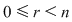 obţinem că : obţinem că : 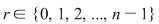
Vom nota 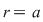 mod mod 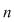 ( ( 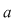 modulo modulo 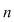 ) )
Prin urmare, dacă 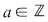 şi şi 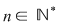 , , 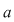 mod mod 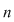 este restul împărţirii lui este restul împărţirii lui 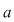 la la 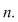
De exemplu : 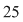 mod mod 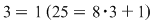 , iar , iar 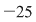  mod mod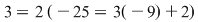
În acest context, prin clasa de resturi modulo 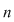 a numărului întreg a numărului întreg 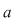 , notată , notată 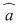 , vom înţelege: , vom înţelege:
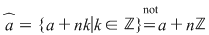 şi ţinînd cont de teorema împărţirii cu rest a lui şi ţinînd cont de teorema împărţirii cu rest a lui 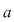 la la 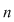 avem succesiv: avem succesiv:
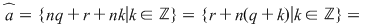
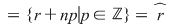 , adică , adică 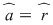 sau sau 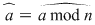
Folosind acest rezultat, dacă 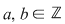 şi şi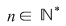 , deducem că urmatoarele afirmaţii sunt echivalente: , deducem că urmatoarele afirmaţii sunt echivalente:
1) 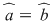
2) 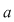 şi şi 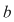 dau acelaşi rest prin împărţirea la dau acelaşi rest prin împărţirea la 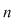
3) 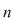 divide divide 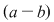
Se mai scrie, în aceste situaţii, că 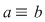 (mod (mod 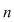 ) şi se citeşte: ) şi se citeşte: 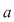 congruent cu congruent cu 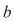 modulo modulo 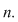
Mulţimea claselor de resturi modulo 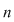 se notează: se notează: 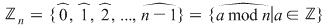 şi pe această mulţime se definesc operaţiile de adunare şi înmulţire a claselor de resturi modulo şi pe această mulţime se definesc operaţiile de adunare şi înmulţire a claselor de resturi modulo 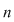 : :
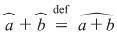
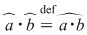 , prin orice , prin orice 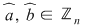
Aceste operaţii sunt bine definite (nu depind de alegerea reprezentanţilor) deoarece, pentru orice 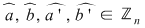 cu cu 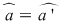 şi şi 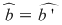 avem (folosind cele 3 echivalenţe) : avem (folosind cele 3 echivalenţe) :
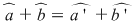 şi şi 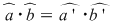
Bibliografie
| 1. Structuri algebrice fundamentale - Otarasanu I. - Editura: Junior - Bucuresti (anul 2000) | | 2. Bac 2003 - Borcea C., Cavachi C., Enescu A., Otarasanu I., Schiopu D. - Editura: Ager (anul 2003) | | 3. Sisteme de ecuatii liniare - Ganga M. - Editura: Mathpress (anul 1996) |
|