Definitii echivalente pentru continuitatea unei functii intr-un punct
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Continuitatea unei functii intr-un punct: scurt istoric, exemle de functii ale caror grafice sunt “intrerupte” sau au “salturi”, definitie punct de acumulare, definitie continuitate intr-un punct, teorema de caracterizare cu siruri, definitie punct de discontinuitate, definitie punct de discontinuitate de prima speta, definitie punct de discontinuitate de a doua speta, 4 exemple.
Domenii: Functii continue
Observaţii
1) Putem vorbi de continuitate doar în punctele domeniului de definiţie al funcţiei.
2) Dacă 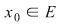 este un punct izolat al lui este un punct izolat al lui 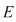 atunci atunci 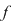 este continuă în este continuă în 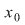 . .
3) Dacă 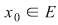 este un punct de acumulare, adică este un punct de acumulare, adică 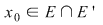 (cu (cu 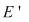 reprezentând mulţimea punctelor de acumulare a mulţimii reprezentând mulţimea punctelor de acumulare a mulţimii 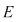 ), studiul continuităţii funcţiei ), studiul continuităţii funcţiei 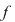 în în 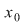 revine la cercetarea existenţei limitei în revine la cercetarea existenţei limitei în 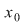 şi compararea ei cu valoarea funcţiei în şi compararea ei cu valoarea funcţiei în 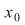 . .
4) Dacă 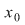 este punct de acumulare al lui este punct de acumulare al lui 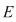 la dreapta (respectiv stânga), atunci : la dreapta (respectiv stânga), atunci :
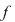 continuă în continuă în 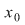 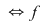 continuă la dreapta (respectiv la stânga) în continuă la dreapta (respectiv la stânga) în 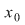 . .
Teoremă (de caracterizare a continuităţii)
Fie 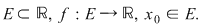 Următoarele afirmaţii sunt echivalente: Următoarele afirmaţii sunt echivalente:
1) 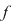 este continuă in este continuă in 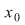 ; ;
2) 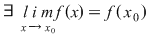
3) 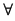 şir şir 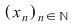 din din 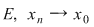 rezultă rezultă 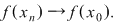
Din teoremă putem trage următoarele concluzii:
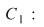 Pentru a arăta că o funcţie este continuă într-un punct Pentru a arăta că o funcţie este continuă într-un punct 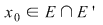 arătăm că: arătăm că:
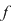 continuă în continuă în 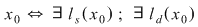 şi şi 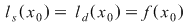 unde unde
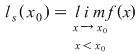
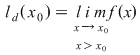
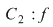 nu este continuă în nu este continuă în 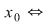 nu există nu există 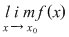 sau sau 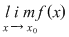 există, dar este diferită de există, dar este diferită de 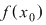 . .
Definiţie : Fie funcţia : 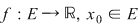 un punct în care un punct în care 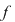 este discontinuă. este discontinuă.
a) 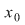 este un punct de discontinuitate de prima speţă al funcţiei este un punct de discontinuitate de prima speţă al funcţiei 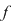 dacă limitele laterale ale funcţiei dacă limitele laterale ale funcţiei 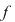 în în 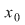 există şi sunt finite. există şi sunt finite.
b) 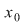 este punct de discontinuitate de speţa a doua dacă nu este punct de discontinuitate de prima speţă (cel puţin o limită laterală este infinită sau nu există). este punct de discontinuitate de speţa a doua dacă nu este punct de discontinuitate de prima speţă (cel puţin o limită laterală este infinită sau nu există).
|