Definitii echivalente pentru continuitatea unei functii intr-un punct
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Continuitatea unei functii intr-un punct: scurt istoric, exemle de functii ale caror grafice sunt “intrerupte” sau au “salturi”, definitie punct de acumulare, definitie continuitate intr-un punct, teorema de caracterizare cu siruri, definitie punct de discontinuitate, definitie punct de discontinuitate de prima speta, definitie punct de discontinuitate de a doua speta, 4 exemple.
Domenii: Functii continue
Se observă că reprezentarea grafică se întrerupe în punctele de abscisă 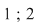 respectiv respectiv 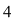 . Vrem să vedem ce se întâmpla cu valorile funcţiei în jurul acestor puncte. Vom analiza comportarea valorilor lui . Vrem să vedem ce se întâmpla cu valorile funcţiei în jurul acestor puncte. Vom analiza comportarea valorilor lui 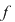 în jurul punctului de abscisă 1. în jurul punctului de abscisă 1.
Observăm că dacă 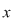 tinde către tinde către 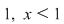 ( ( 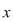 se apropie de se apropie de 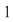 cu valori mai mici decât cu valori mai mici decât 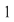 ), valorile lui ), valorile lui 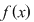 tind către valoarea lui tind către valoarea lui 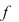 în în 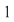 , adică , adică 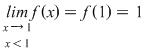 . .
Dacă 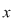 tinde către tinde către 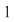 , , 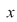 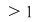 ( ( 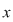 se apropie de se apropie de 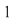 , cu valori mai mari decât , cu valori mai mari decât 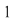 ), valorile lui ), valorile lui 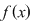 tind către valoare lui tind către valoare lui 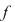 în în 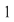 , adică tind către , adică tind către 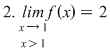 . .
"Saltul" din jurul punctului de abscisă 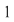 se datorează faptului că limitele laterale în se datorează faptului că limitele laterale în 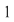 sunt diferite. sunt diferite.
Să studiem comportamentul lui 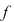 în jurul punctului de abscisă în jurul punctului de abscisă 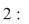
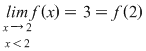 , deci nu avem "salt" în , deci nu avem "salt" în 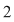 . .
Dacă alegem un punct din domeniu, diferit de 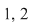 sau sau 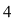 adică adică 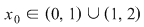 constatăm că constatăm că 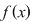 tinde către tinde către 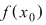 când când 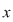 tinde tinde 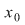 . .
Punctul de abscisă 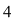 este punct izolat în domeniul de definiţie al funcţiei este punct izolat în domeniul de definiţie al funcţiei 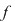 , deoarece funcţia , deoarece funcţia 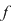 nu este definită în alte puncte dintr-o vecinătate a lui nu este definită în alte puncte dintr-o vecinătate a lui 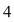 . .
Graficul " nu se întrerupe " în 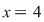 . .
Vom defini continuitatea unei funcţii într-un punct .
Definiţie : Fie o funcţie reală 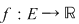 cu cu 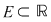 şi un punct şi un punct 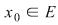 . .
O funcţie 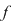 se numeşte continuă în punctul se numeşte continuă în punctul 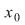 dacă pentru orice vecinătate dacă pentru orice vecinătate 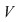 a punctului a punctului 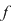 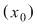 există o vecinătate există o vecinătate 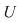 a punctului a punctului 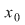 astfel încât din faptul că astfel încât din faptul că 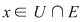 să rezulte să rezulte 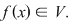
Pe scurt:
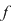 continuă în continuă în 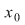 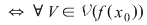 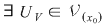 astfel încât astfel încât 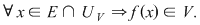
Dacă 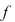 nu este continuă în nu este continuă în 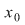 atunci atunci 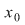 se numeşte punct de discontinuitate. se numeşte punct de discontinuitate.
|