 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Definitii echivalente pentru continuitatea unei functii intr-un punct
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Continuitatea unei functii intr-un punct: scurt istoric, exemle de functii ale caror grafice sunt “intrerupte” sau au “salturi”, definitie punct de acumulare, definitie continuitate intr-un punct, teorema de caracterizare cu siruri, definitie punct de discontinuitate, definitie punct de discontinuitate de prima speta, definitie punct de discontinuitate de a doua speta, 4 exemple.
Domenii: Functii continue
 DEFINIŢII ECHIVALENTE PENRU CONTINUITATEA
DEFINIŢII ECHIVALENTE PENRU CONTINUITATEA  UNEI FUNCŢII ÎNTR-UN PUNCT UNEI FUNCŢII ÎNTR-UN PUNCT
Ideea de continuitate a unei funcţii s-a desprins din reprezentările intuitive asupra proceselor în desfăşurarea cărora nu apar salturi, ruperi. Noţiunea matematică de continuitate cere o definiţie precisă, care să conducă prin raţionamente corecte la degajarea proprietăţilor funcţiilor continue, importante în aplicaţii şi în dezvoltări teoretice ulterioare. Conceptul de funcţie continuă s-a definit relativ târziu şi este datorat în principal lui A. Cauchy (1789-1857), B. Bolzano (1781-1848) şi G. Darboux (1842-1917).
Pentru înţelegerea naturii de funcţie continuă într-un punct vom considera câteva exemple:
1) Presupunem că pe o axă se mişcă uniform un mobil care la momentul 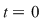 se află în origine. Dacă viteza, presupusă constantă, a mobilului este se află în origine. Dacă viteza, presupusă constantă, a mobilului este 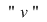 , atunci, notând cu , atunci, notând cu 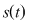 distanţa parcursă de mobil în timpul distanţa parcursă de mobil în timpul 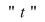 , rezultă că , rezultă că 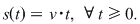
Graficul funcţiei corespunzătoare acestui fenomen 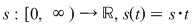 este următorul: este următorul:
|