 Optiuni  Inapoi la biblioteca |
Numere complexe. Forma algebrica a unui numar complex
Autor: Iulia Liberis
Descriere: articol pentru Clasa a X-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Definirea numerelor complexe ca perechi de numere reale. Suma, produsul a doua numere complexe. Numarul i. Forma algebrica a unui numar complex.
Domenii: ---
Numere complexe. Forma algebrică a unui număr complex
În studiul algebrei se observă o continuă generalizare a noţiunii de număr. În clasele primare, elevul studiază numerele naturale, apoi în gimnaziu se trece la noţiunea de număr întreg şi număr raţional. Extinderea noţiunii de număr întreg s-a impus, printre altele, şi de necesitatea rezolvării unor ecuaţii. De expemplu ecuaţia 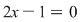 nu are soluţii întregi (în nu are soluţii întregi (în 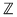 ) , dar are soluţia ) , dar are soluţia 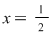 raţională (în raţională (în  ). ).
Ecuaţia 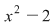 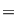 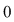 nu are soluţii raţionale (în nu are soluţii raţionale (în 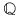 ), dar are soluţiile ), dar are soluţiile 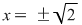 iraţionale iraţionale 
Astfel mulţimea numerelor reale este constituită din mulţimea numerelor raţionale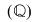 şi iraţionale şi iraţionale  Nici această ultimă mulţime Nici această ultimă mulţime 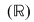 nu poate acoperi întreaga gamă de probleme, în sensul că există ecuaţii care nu au soluţii în mulţimea numerelor reale. nu poate acoperi întreaga gamă de probleme, în sensul că există ecuaţii care nu au soluţii în mulţimea numerelor reale.
O ecuaţie simplă, cu coeficienţi reali, cum este 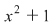 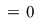 , nu are soluţii în , nu are soluţii în 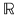 , deoarece niciun număr real nu poate avea pătratul negativ , deoarece niciun număr real nu poate avea pătratul negativ 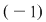 . Se impune extinderea mulţimii numerelor reale, definindu-se o mulţime de numere mai bogată, în care ecuaţia . Se impune extinderea mulţimii numerelor reale, definindu-se o mulţime de numere mai bogată, în care ecuaţia 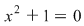 să aibă soluţie. să aibă soluţie.
Forma algebrică a unui număr complex
Fie 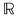 mulţimea numerelor reale. mulţimea numerelor reale.  este produsul cartezian al mulţimii este produsul cartezian al mulţimii 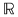 cu ea însăşi, cu ea însăşi, 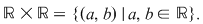
Bibliografie
| 1. Manual pentru clasa a X-a - Ganga M. |
|