 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Un semigrup remarcabil
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 07 Feb 2008, nivel de dificultate  . .
Semigrupul relatiilor binare ale unei multimi: definitie, asociativitatea compunerii, existenta elementului neutru—diagonala acelei multimi.
Domenii: Lege de compozitie interna
Propoziţia 2.2:
1.Dacă 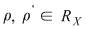 atunci: atunci: 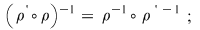
2.Dacă 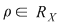 atunci : atunci : 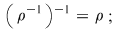
3.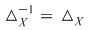
Demonstraţie :
1. Dacă 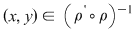 atunci atunci  , deci există , deci există 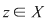 cu cu 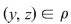 şi şi 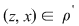 . De aici rezultă că . De aici rezultă că 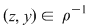 şi şi 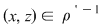 , adică , adică 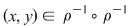 şi deci incluziunea: şi deci incluziunea: 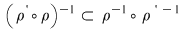
Reciproc, dacă 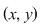 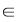 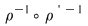 , atunci există , atunci există 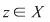 cu cu 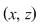 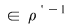 şi şi 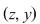 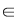 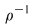 , adică , adică 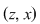 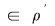 şi şi 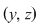 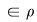 . De aici . De aici 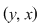 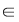 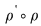 şi prin urmare şi prin urmare 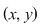 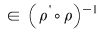 , deci incluziunea: , deci incluziunea: 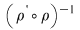 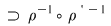 . .
2. Dacă 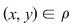 atunci atunci 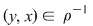 şi şi 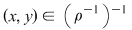 , deci: , deci: 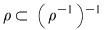
Reciproc, dacă 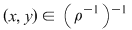 atunci atunci 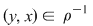 şi şi 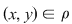 deci deci 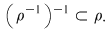
3.Deoarece 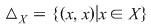 rezultă că rezultă că 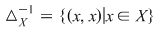 deci deci 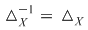 . .
În finalul articolului vom depista situaţiile în care o relaţie binară 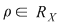 este relaţie de echivalenţă. este relaţie de echivalenţă.
Fie, deci, 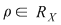 o relaţie binară pe o relaţie binară pe 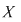 . .
Dacă 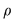 este reflexivă, atunci este reflexivă, atunci 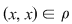 oricare ar fi oricare ar fi 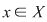 , adică , adică 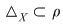 . .
Dacă, în plus, relaţia 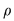 este simetrică, atunci oricare ar fi este simetrică, atunci oricare ar fi 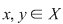 cu cu 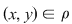 rezultă rezultă 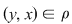 şi cum şi cum 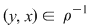 rezultă că rezultă că 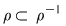 . Dacă . Dacă 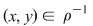 atunci atunci 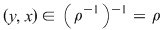 adică adică 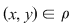 şi prin urmare, şi prin urmare, 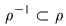 , deci , deci 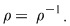
Dacă relaţia 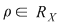 este tranzitivă, atunci oricare ar fi este tranzitivă, atunci oricare ar fi 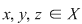 cu cu 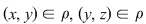 rezultă rezultă 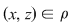 , adică , adică 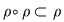 , iar dacă , iar dacă 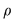 este reflexivă este reflexivă 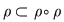 şi prin urmare şi prin urmare 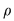 este o relaţie de echivalenţă dacă şi numai dacă: este o relaţie de echivalenţă dacă şi numai dacă:
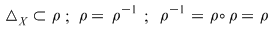
Se observă că relaţiile de echivalenţă ale mulţimii 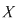 sunt elemente idempotente ale subgrupului sunt elemente idempotente ale subgrupului 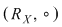 . .
Observaţie:
Dacă 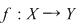 este o funcţie, graficul său: este o funcţie, graficul său:
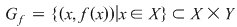 are proprietatea că are proprietatea că 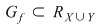
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
Bibliografie
| 1. Elemente de teoria semigrupurilor - Nastasescu C., Otarasanu I. - Editura: Rotech-Pro - Bucuresti (anul 1999) |
|