Structuri algebrice pregrupale
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 27 Apr 2009, nivel de dificultate  . .
Conceptul de structura algebrica—scurt istoric. Operatii algebrice: definitie si exemple. Conceptele de grupoid, subgrupoid, parte stabila, monoid, semigrup, quasigrup, bucla(loop) cu exemple. Morfisme si izomorfisme. Aplicatii diverse.
Domenii: Grupuri
Fie 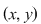 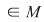 un element inversabil. Aceasta înseamnă că există un element inversabil. Aceasta înseamnă că există 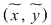  astfel încât: astfel încât: 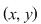  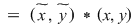  . Rezultă egalităţile: . Rezultă egalităţile:
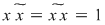 şi şi
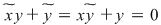 . Primele egalităţi arată că . Primele egalităţi arată că 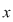 este inversabil în monoidul este inversabil în monoidul 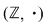 deci deci  . Dacă . Dacă 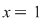 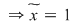 şi apoi şi apoi  , iar dacă , iar dacă 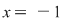 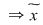 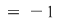 şi apoi şi apoi 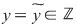 . .
Deci, elementele inversabile din monoidul  sunt cele de forma sunt cele de forma 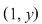 sau sau 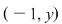 , unde , unde 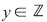 . .
X. Fie 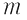 mulţimea matricilor mulţimea matricilor 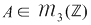 de forma: de forma:
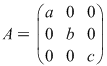
cu 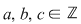 . Să se arate că . Să se arate că 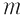 este parte stabilă a lui este parte stabilă a lui 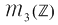 în raport cu înmulţirea matricilor, că formează monoid în raport cu operaţia indusă şi să se determine elementele simetrizabile ale monoidului în raport cu înmulţirea matricilor, că formează monoid în raport cu operaţia indusă şi să se determine elementele simetrizabile ale monoidului 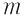 . .
Soluţie:
Se constată uşor că 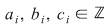 , , 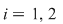 . Atunci . Atunci
 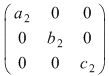 
de unde rezultă că 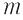 este parte stabilă a lui este parte stabilă a lui 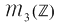 faţă de înmulţire. faţă de înmulţire.
Înmulţirea este asociativă în  , deoarece este asociativă în , deoarece este asociativă în 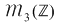 . .
Matricea 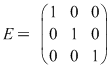 aparţine lui aparţine lui  şi este element neutru faţă de înmulţirea din mulţimea şi este element neutru faţă de înmulţirea din mulţimea 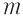 . Aşadar, . Aşadar, 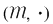 este un monoid (care este şi comutativ). Ţinând seama de modul cum se realizează înmulţirea în mulţimea este un monoid (care este şi comutativ). Ţinând seama de modul cum se realizează înmulţirea în mulţimea  , deducem că o matrice: , deducem că o matrice:
 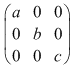 este inversabilă în este inversabilă în 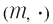 dacă şi numai dacă dacă şi numai dacă 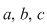 sunt inversabile în monoidul sunt inversabile în monoidul 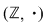 , adică dacă şi numai dacă , adică dacă şi numai dacă 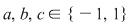 . .
Rezultă că există  elemente inversabile în elemente inversabile în 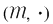 . Acestea sunt următoarele matrici: . Acestea sunt următoarele matrici:
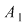 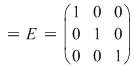
Materiale Didactice Asemanatoare
 Doua probleme de grupuri Doua probleme de grupuri
|