 Optiuni  Inapoi la biblioteca |
Permutari. Notiunea de permutare
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 25 Apr 2008, nivel de dificultate  . .
Definitia permutarii. Gradul permutarii. Cardinalul multimii permutarilor de grad dat. Permutarea identica. Exemple.
Domenii: ---
Permutări. Noţiunea de permutare
Am făcut cunoştinţă cu noţiunea de permutare încă din clasa a X-a. Fiind dată o mulţime finită 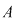 , având , având 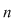 elemente, ea se poate ordona în diverse moduri, în sensul că fiecărui element al său i se asociază un anumit număr de la elemente, ea se poate ordona în diverse moduri, în sensul că fiecărui element al său i se asociază un anumit număr de la 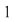 la la 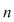 , numit rangul elementului. , numit rangul elementului.
Exemplu:
Mulţimea 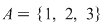 are trei elemente ce pot fi ordonate în următoarele moduri: are trei elemente ce pot fi ordonate în următoarele moduri:  , , 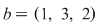 , , 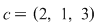 , ,  , , 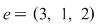 , , 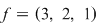 . .
În prima permutare notată 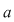 , , 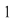 are rangul are rangul 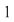 , ,  are rangul are rangul 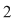 şi şi 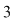 are rangul are rangul  . În cea de-a doua permutare, notată . În cea de-a doua permutare, notată 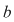 , , 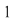 are rangul are rangul 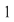 , , 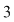 are rangul are rangul 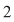 şi şi 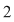 are rangul are rangul 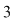 . .
Noţiunea de permutare.
Să notăm cu 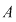 mulţimea primelor mulţimea primelor 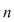 numere naturale, adică numere naturale, adică 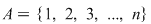 . Fie . Fie 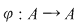 o bijecţie a mulţimii o bijecţie a mulţimii 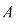 şi notăm şi notăm  , , 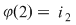 , ..., , ..., 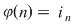 . . 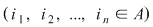 . .
Funcţia 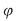 poate fi reprezentată printr-un tablou cu două linii: poate fi reprezentată printr-un tablou cu două linii:
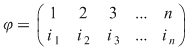
Prima linie indică poziţia 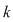 pe care se află elementul pe care se află elementul 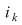 din linia a doua, sau, cu alte cuvinte, locul ocupat de elementul din linia a doua, sau, cu alte cuvinte, locul ocupat de elementul 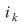 în şirul finit în şirul finit 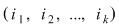 . .
Definiţie: Fie mulţimea 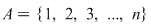 . O funcţie bijectivă . O funcţie bijectivă  se numeşte permutare de gradul se numeşte permutare de gradul 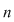 . Mulţimea tuturor permutărilor de gradul . Mulţimea tuturor permutărilor de gradul 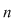 . Permutările din . Permutările din 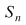 le vom nota cu litere greceşti le vom nota cu litere greceşti 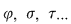 (citim: fi, sigma, tau, ...). (citim: fi, sigma, tau, ...).
Bibliografie
| 1. Manual pentru clasa a XI-a - Editura: Didactica si Pedagogica (anul 1982) |
|