Metoda bazata pe teorema Kronecker-Capelli si teorema lui Rouche de rezolvare a sistemelor liniare de m ecuatii si n necunoscute
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 09 Iul 2008, nivel de dificultate  . .
Enunt teorema Kronecker-Capelli. Definitii minor principal, necunoscute principale, necunoscute secundare, ecuatii principale, ecuatii secundare, minor caracteristic. Teorema lui Rouche, enunt. Algoritm pentru rezolvarea sistemelor liniare. 2 exemple.
Domenii: ---
Metodă bazată pe teorema Kronecker-Capelli şi teorema Rouché de rezolvare a sistemelor liniare de 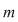 ecuaţii cu ecuaţii cu 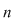 necunoscute necunoscute
Presupunem că rangul matricei sistemului este 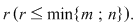
Teorema Kronecker- Capelli
Un sistem de ecuaţii liniare este compatibil dacă şi numai dacă rangul matricei sistemului este egal cu rangul matricei extinse.
Definiţie:
Fie 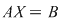 un sistem liniar scris în formă matriceală. Presupunem că matricea sistemului un sistem liniar scris în formă matriceală. Presupunem că matricea sistemului 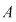 are rangul are rangul 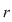 . .
Din matricea sistemului alegem un minor nenul de ordin 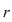 pe care îl numim minor principal şi îl notăm pe care îl numim minor principal şi îl notăm 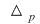 . Necunoscutele ale căror coeficienţi sunt coloane în . Necunoscutele ale căror coeficienţi sunt coloane în 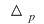 se numesc necunoscute principale. Celelalte necunoscute, dacă există, se numesc necunoscute secundare. se numesc necunoscute principale. Celelalte necunoscute, dacă există, se numesc necunoscute secundare.
Ecuaţiile ale căror coeficienţi sunt linii în 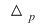 se numesc ecuaţii principale. se numesc ecuaţii principale.
Celelalte ecuaţii, dacă există, se numesc ecuaţii secundare.
- Pentru determinarea rangului matricei extinse se construieşte un minor caracteristic  astfel: bordăm determinantul principal astfel: bordăm determinantul principal 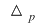 pe "orizontală" cu coeficienţii necunoscutelor principale dintr-o ecuaţie secundară şi pe "verticală" cu elementele corespunzătoare ale coloanei termenilor liberi. pe "orizontală" cu coeficienţii necunoscutelor principale dintr-o ecuaţie secundară şi pe "verticală" cu elementele corespunzătoare ale coloanei termenilor liberi.
|