 Optiuni  Inapoi la biblioteca |
Metoda bazata pe teorema Kronecker-Capelli si teorema lui Rouche de rezolvare a sistemelor liniare de m ecuatii si n necunoscute
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 09 Iul 2008, nivel de dificultate  . .
Enunt teorema Kronecker-Capelli. Definitii minor principal, necunoscute principale, necunoscute secundare, ecuatii principale, ecuatii secundare, minor caracteristic. Teorema lui Rouche, enunt. Algoritm pentru rezolvarea sistemelor liniare. 2 exemple.
Domenii: ---
Teorema lui Rouché
Un sistem de ecuaţii liniare este compatibil, dacă şi numai dacă toţi minorii caracteristici (dacă există) sunt nuli.
Observaţie:
Dacă sistemul de ecuaţii liniare nu are minori caracteristici, atunci el este compatibil (nu are minori caracteristici 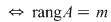 , adică are rangul egal cu numărul de ecuaţii, şi , adică are rangul egal cu numărul de ecuaţii, şi 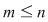 ). ).
Etape de rezolvare:
1) Se determină rangul matricei sistemului 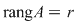 şi se stabileşte dacă sistemul este compatibil sau nu (folosind Kronecker- Capelli sau Rouché ) şi se stabileşte dacă sistemul este compatibil sau nu (folosind Kronecker- Capelli sau Rouché )
- Dacă 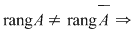 sistemul este incompatibil sistemul este incompatibil
- Dacă 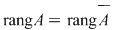 atunci atunci
2) Se alege un minor principal 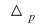 şi se specifică ecuaţiile principale, ecuaţiile secundare, necunoscutele principale şi necunoscutele secundare. şi se specifică ecuaţiile principale, ecuaţiile secundare, necunoscutele principale şi necunoscutele secundare.
3) Se rezolvă prin Cramer sistemul format din ecuaţiile principale în care necunoscutele secundare se trec în membrul al doilea (în dreapta egalului).
Se vor obţine necunoscutele principale exprimate liniar în funcţie de necunoscutele secundare (acestea rămânând parametri arbitrari).
|