Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
Prezentăm în continuare scrierea uzuală pentru polinoame, care se dovedeşte mai comodă în calcule.
Notăm prin 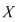 polinomul polinomul 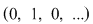 care se numeşte nedeterminata care se numeşte nedeterminata 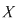 . Înmulţirea polinoamelor ne dă: . Înmulţirea polinoamelor ne dă: 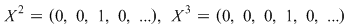 şi, mai general, şi, mai general, 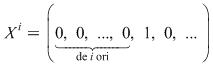 . Fie . Fie 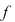 un polinom de grad un polinom de grad 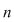 ai cărui coeficienţi sunt ai cărui coeficienţi sunt 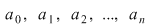 , adică , adică 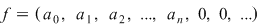 . .
Putem scrie 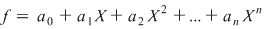 , obţinând astfel scrierea obişnuită a unui polinom. , obţinând astfel scrierea obişnuită a unui polinom.
Definiţie: Inelul 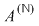 se numeşte inelul polinoamelor în nedeterminata se numeşte inelul polinoamelor în nedeterminata 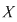 cu coeficienţi în inelul cu coeficienţi în inelul 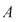 şi se notează prin şi se notează prin 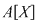 . .
Inelul 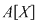 se mai numeşte şi inelul polinoamelor într-o nedeterminată cu coeficienţi în se mai numeşte şi inelul polinoamelor într-o nedeterminată cu coeficienţi în 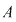 . Un polinom de grad . Un polinom de grad 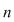 în nedeterminata în nedeterminata 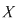 se scrie condensat: se scrie condensat:
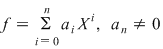
Teorema 3: Dacă 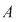 este un inel comutativ şi este un inel comutativ şi 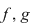 polinoame din polinoame din 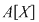 , atunci: , atunci:
1) 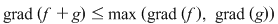
2) 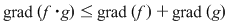
3) dacă, în plus, 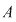 este domeniu de integritate, avem este domeniu de integritate, avem 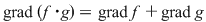
Demonstraţie:
Dacă cel mult unul dintre polinoamele 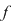 sau sau 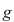 este nul, atunci afirmaţiile teoremei sunt, evident, adevărate, având în vedere convenţiile privind calculele cu este nul, atunci afirmaţiile teoremei sunt, evident, adevărate, având în vedere convenţiile privind calculele cu 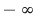 . Dacă . Dacă 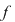 şi şi 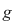 sunt nenule, afirmaţiile de la punctele 1) şi 2) rezultă din definiţia sumei şi produsului a două polinoame. sunt nenule, afirmaţiile de la punctele 1) şi 2) rezultă din definiţia sumei şi produsului a două polinoame.
Pentru afirmaţia de la punctul 3), fie 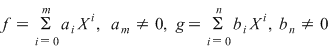 . Cum . Cum 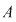 este domeniu de integritate, coeficientul dominant al produsului este domeniu de integritate, coeficientul dominant al produsului 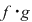 este este 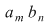 care este nenul. Deci, în acest caz, care este nenul. Deci, în acest caz, 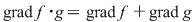 . .
Corolar: Dacă 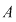 este un domeniu de integritate, atunci inelul polinoamelor este un domeniu de integritate, atunci inelul polinoamelor 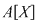 este domeniu de integritate. este domeniu de integritate.
Demonstraţia: Rezultă din punctul 3) al teoremei precedente.
|