Inele de polinoame. Proprietati aritmetice
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 06 Feb 2008, nivel de dificultate  . .
Polinoame cu coeficienti complecsi. Definirea sumei si a produsului a doua polinoame. Inelul polinoamelor peste un inel comutativ. Unitati intr-un inel de polinoame. Valoarea unui polinom. Functie polinomiala. Teorema impartirii cu rest; exemple. Divizibilitatea in inele de polinoame. Cel mai mare divizor comun a doua polinoame. Polinoame prime intre ele. Radacinile unui polinom; teorema lui Bezout; schema lui Horner; exemple.
Domenii: ---
II. Mulţimea 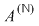 împreună cu înmulţirea este monoid comutativ. împreună cu înmulţirea este monoid comutativ.
Într-adevăr, înmulţirea are proprietăţile:
1) este asociativă, adică 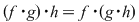 , oricare ar fi , oricare ar fi 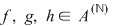 ; ;
2) are element neutru 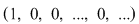 ; ;
3) este comutativă, adică 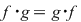 , oricare ar fi , oricare ar fi 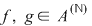 . .
III. Înmulţirea este distributivă faţă de adunare, adică 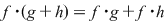 şi şi 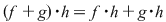 , oricare ar fi , oricare ar fi 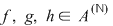 . .
Demonstrarea este asemănătoare ca în cazul polinoamelor cu coeficienţi complecşi.
Ţinând cont de proprietăţile I, II şi III, avem:
Teorema 1: Mulţimea 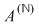 împreună cu adunarea şi înmulţirea este un inel comutativ. împreună cu adunarea şi înmulţirea este un inel comutativ.
Definiţie: Elementele inelului de la teorema precedentă se numesc polinoame cu coeficienţi în inelul comutativ 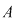 . .
Dacă 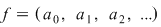 este un polinom nenul, atunci este un polinom nenul, atunci 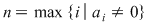 se numeşte gradul polinomului se numeşte gradul polinomului 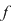 . Gradul unui polinom . Gradul unui polinom 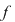 se notează prin se notează prin 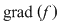 , iar coeficientul , iar coeficientul 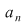 unde unde 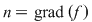 , se numeşte coeficientul dominant al polinomului , se numeşte coeficientul dominant al polinomului 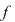 . Pentru polinomul nul, convenim să considerăm gradul său ca fiind . Pentru polinomul nul, convenim să considerăm gradul său ca fiind 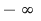 , adoptând convenţiile uzuale, şi anume: , adoptând convenţiile uzuale, şi anume: 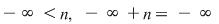 , pentru orice număr natural , pentru orice număr natural 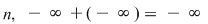 . Dacă . Dacă 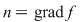 , atunci , atunci 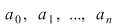 se numesc coeficienţii polinomului se numesc coeficienţii polinomului 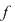 . .
Teorema 2: Dacă 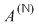 este un inel comutativ, atunci următoarele afirmaţii sunt adevărate: este un inel comutativ, atunci următoarele afirmaţii sunt adevărate:
1) Funcţia 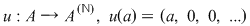 este morfism injectiv de inele. este morfism injectiv de inele.
2) Operaţiile algebrice ale lui 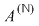 induc operaţii algebrice pe induc operaţii algebrice pe 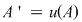 , în raport cu care , în raport cu care 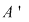 este inel comutativ. este inel comutativ.
3) Inelele 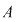 şi şi 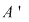 sunt izomorfe. sunt izomorfe.
Demonstraţie:
1) Dacă 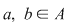 , atunci , atunci 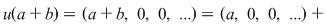
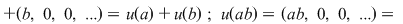
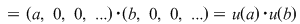 si si 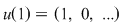
Mai mult, dacă 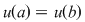 , atunci , atunci 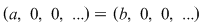 şi deci şi deci 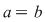
2) Dacă 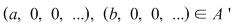 , atunci , atunci 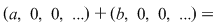
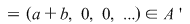 si si 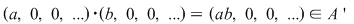
Deci adunarea şi înmulţirea din 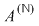 induc operaţii algebrice pe induc operaţii algebrice pe 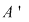 . Rezultă imediat că . Rezultă imediat că 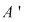 împreună cu operaţiile induse este inel comutativ. împreună cu operaţiile induse este inel comutativ.
3) Morfismul injectiv 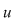 dă izomorfismul căutat între inelele dă izomorfismul căutat între inelele 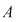 şi şi 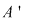 . .
Izomorfismul de la punctul 3) al teoremei precedente permite să se identifice elementul 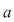 din din 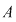 cu imaginea sa prin cu imaginea sa prin 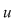 , adică polinomul , adică polinomul 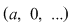 din din 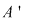 . Polinoamele . Polinoamele 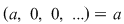 se numesc constante. se numesc constante.
|