 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Formula de integrare prin parti
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Formula de integrare prin parti: teorema cu demonstratie; orice functie continua cu exceptia unui numar finit de puncte, in care are discontinuitati de prima speta, este integrabila, demonstratie, exemplu; teorema (formula de schimbare de variabila) cu demonstratie, exemple.
Domenii: Functii integrabile Riemann
2. Tehnica dată de teoremă se reţine astfel: facem schimbarea de variabilă 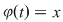 , prin diferenţierea formală avem , prin diferenţierea formală avem 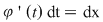 . .
3. Integrala din membrul drept al formulei 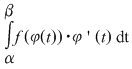 se face "de la se face "de la 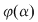 la la 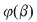 " putându-se întâmpla ca " putându-se întâmpla ca 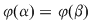 sau ca sau ca 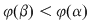 . .
Astfel: 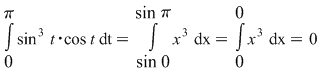
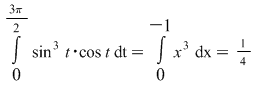
4. Se ştie că dacă 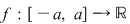 este o funcţie integrabilă impară, atunci este o funcţie integrabilă impară, atunci 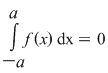 . Având în vedere ipotezele teoremei pentru cazul în care funcţia . Având în vedere ipotezele teoremei pentru cazul în care funcţia 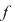 este continuă şi impară, rezultatul poate fi obţinut făcând schimbarea de variabilă: este continuă şi impară, rezultatul poate fi obţinut făcând schimbarea de variabilă:
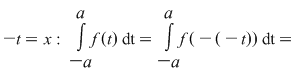
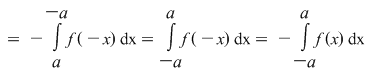 , de unde rezultă că , de unde rezultă că 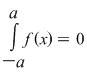 . La fel se poate arăta că dacă . La fel se poate arăta că dacă 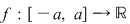 este continuă şi pară, atunci este continuă şi pară, atunci 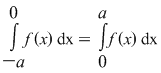 şi deci şi deci 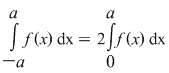 . .
5. În unele exemple se observă direct prezenţa unor funcţii de integrat de forma 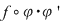 . În cele mai multe cazuri se încearcă obţinerea unei asemenea forme prin transformări elementare. Astfel, pentru calculul integralei . În cele mai multe cazuri se încearcă obţinerea unei asemenea forme prin transformări elementare. Astfel, pentru calculul integralei 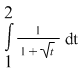 se scrie se scrie 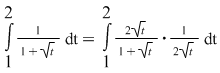 . .
Cu schimbarea de variabilă 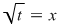 se obţine se obţine 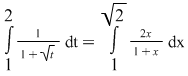 . .
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|