 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Sisteme de ecuatii in Zn
Autor: Ion Otarasanu
Descriere: articol pentru Clasa a XII-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Inelul claselor de resturi : definitie, unitati. Sisteme de ecuatii liniare cu coeficienti in inelul claselor de resturi, exemple. Mica teorema a lui Fermat, exemple.
Domenii: Inele



Cum niciunul dintre coeficienţii sistemului nu este element inversabil în  , rămâne să aplicăm alte metode. Adunăm toate ecuaţiile şi găsim: , rămâne să aplicăm alte metode. Adunăm toate ecuaţiile şi găsim:
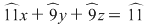 şi cum şi cum  , iar , iar  , obţinem, înmulţind această ecuaţie cu , obţinem, înmulţind această ecuaţie cu  : :
 sau sau  pe care-l substituim în primele două ecuaţii: pe care-l substituim în primele două ecuaţii:
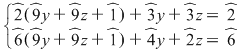



Apoi, substituind pe  în prima şi a treia ecuaţie vom găsi alte triplete şi, în final, substituindu-l în ecuaţiile a doua şi a treia vom gasi, din nou, alte triplete. Verificarea ne va conduce la soluţiile: în prima şi a treia ecuaţie vom găsi alte triplete şi, în final, substituindu-l în ecuaţiile a doua şi a treia vom gasi, din nou, alte triplete. Verificarea ne va conduce la soluţiile:
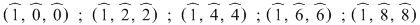
III. Observaţii:
1) Dacă pentru 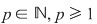 , ,  prim, atunci prim, atunci  este, evident, un corp şi toată teoria sistemelor de ecuaţii liniare studiate în cazul când acestea au coeficienţi complecşi (reali) rămâne valabilă. este, evident, un corp şi toată teoria sistemelor de ecuaţii liniare studiate în cazul când acestea au coeficienţi complecşi (reali) rămâne valabilă.
2) Dacă 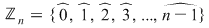 atunci numerele naturale atunci numerele naturale  se numesc reprezentanţii canonici ai claselor de resturi se numesc reprezentanţii canonici ai claselor de resturi  . .
3) Teorema lui Fermat: Dacă  prim şi prim şi  nu divide nu divide  , atunci , atunci 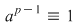 (mod p) (mod p)
Bibliografie
| 1. Structuri algebrice fundamentale - Otarasanu I. - Editura: Junior - Bucuresti (anul 2000) | | 2. Bac 2003 - Borcea C., Cavachi C., Enescu A., Otarasanu I., Schiopu D. - Editura: Ager (anul 2003) | | 3. Sisteme de ecuatii liniare - Ganga M. - Editura: Mathpress (anul 1996) |
|