| |
 Optiuni  Inapoi la biblioteca |
Proprietatile determinantilor - Partea I
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 02 Mai 2008, nivel de dificultate  .
Proprietatile determinantilor: determinantul unei matrice (patratice) este egal cu determinantul matricei transpuse; o matrice cu o linie (coloana) nula are determinantul zero, prin inmultirea unei linii (respectiv coloane) cu un numar determinantul se inmulteste cu acel numar, determinantul nu se schimba prin adunarea la o linie (coloana) a unei combinatii liniare de celelalte linii (respectiv coloane), exemple.
Domenii: ---
Observaţie:
Această proprietate ne permite să transcriem proprietăţile obţinute pentru liniile unui determinant la coloanele sale (şi reciproc).
2. Dacă o matrice are o linie (sau o coloană) cu toate elementele 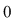 , atunci determinantul ei este egal cu 
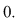
Exemplu:
Fie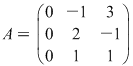 
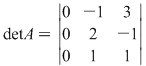
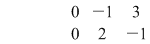
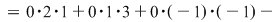
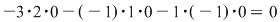
3. Dacă înmulţim toate elementele unei linii (sau ale unei coloane) ale unei matrice cu un număr, valoarea determinantului matricei se înmulţeşte cu acel număr.
Bibliografie
| 1. Manual pentru clasa a XI-a - Editura: Sigma |
|
| |
| |