Continuitatea pe o multime
Autor: Iulia Liberis
Descriere: articol pentru Clasa a XI-a publicat in data de 05 Feb 2008, nivel de dificultate  . .
Definitia continuitatii unei functii pe o multime. Teorema: functiile elementare sunt continue, exemple.
Domenii: Functii continue
Continuitatea pe o mulţime
Definiţie
Spunem că o funcţie 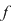 este continuă pe o submulţime a domeniului de definiţie dacă este continuă în fiecare punct al acesteia. este continuă pe o submulţime a domeniului de definiţie dacă este continuă în fiecare punct al acesteia.
Mulţimea punctelor din domeniul de definiţie pe care o funcţie este continuă se numeşte domeniul de continuitate al funcţiei.
Dacă 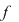 este continuă pe întreg domeniul său de definiţie, spunem că este continuă pe întreg domeniul său de definiţie, spunem că 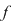 este continuă. este continuă.
Teoremă
Funcţiile elementare (polinomiale, putere, exponenţiale, logaritmice şi trigonometrice) sunt funcţii continue pe întreg domeniul lor de definiţie.
Exemplu
Să se studieze continuitatea funcţiei
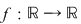 , , 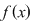 
pe domeniul de definiţie.
Soluţie: Deoarece funcţia 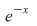 este compunerea dintre două funcţii elementare: este compunerea dintre două funcţii elementare: 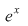 şi şi 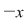  este o funcţie continuă este o funcţie continuă 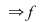 este continuă pe este continuă pe 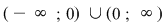 . .
Se studiază continuitatea funcţiei în 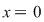 . .
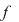 continuă în continuă în 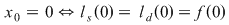
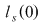 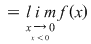 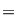 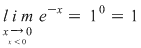
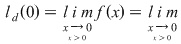 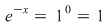
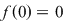
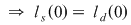
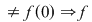 nu este continuă în nu este continuă în 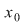 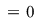 . .
|