 Filtre |
Biblioteca
In cadrul bibliotecii online poti studia 12 articole, 179 lectii.
Articolul zilei: Functii integrabile - Partea II
Funcţii integrabile
(2)
Criterii de integrabilitate.
Cu ajutorul condiţiilor echivalente de integrabilitate se vor putea obţine proprietăţi ale funcţiilor integrabile şi ale integralei, se vor identifica familii de funcţii integrabile.
2.1. Criteriul cu şiruri de sume Riemann.
Teoremă: (criteriul cu siruri de sume Riemann)
Funcţia 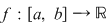 este integrabilă dacă şi numai dacă există un număr real este integrabilă dacă şi numai dacă există un număr real 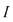 şi pentru orice şir şi pentru orice şir 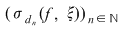 de sume Riemann astfel încât de sume Riemann astfel încât 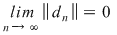 avem avem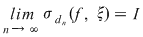 . Atunci . Atunci 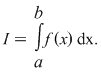
Demonstratie:
Dacă funcţia 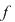 este integrabilă, atunci există un număr real este integrabilă, atunci există un număr real 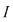 şi pentru orice număr şi pentru orice număr 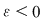 există există 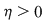 astfel încât pentru orice sumă Riemann astfel încât pentru orice sumă Riemann 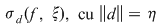 , avem , avem 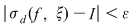 . Atunci, dacă . Atunci, dacă 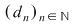 este un şir de diviziuni cu este un şir de diviziuni cu 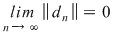 , există , există 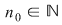 şi pentru orice şi pentru orice 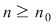 , avem , avem 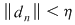 . Rezultă că . Rezultă că 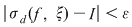 . Recapitulând, pentru orice . Recapitulând, pentru orice 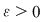 există există 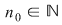 astfel încât pentru orice astfel încât pentru orice 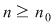 avem avem 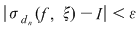 . Aceasta înseamnă . Aceasta înseamnă 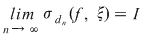 . .
Reciproc, să presupunem că există un număr real 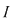 şi că pentru orice şir de sume Riemann şi că pentru orice şir de sume Riemann 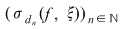 , cu , cu 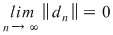 avem avem 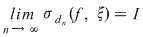 . Să presupunem că funcţia . Să presupunem că funcţia 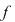 nu este integrabilă. Atunci, pentru numărul nu este integrabilă. Atunci, pentru numărul 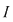 există există 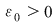 şi, pentru orice număr şi, pentru orice număr 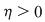 , există o sumă Riemann , există o sumă Riemann 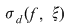 cu cu 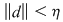 , astfel încât , astfel încât 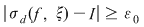 . Alegând . Alegând 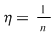 , rezultă că există , rezultă că există 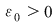 şi pentru orice şi pentru orice 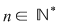 , există , există 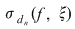 o sumă Riemann cu o sumă Riemann cu 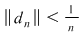 , astfel încât , astfel încât 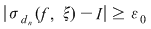 . Atunci şirul . Atunci şirul 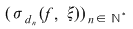 nu converge către nu converge către 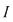 , cu toate că , cu toate că 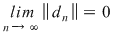 , ceea ce contrazice ipoteza. Funcţia , ceea ce contrazice ipoteza. Funcţia 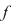 este integrabilă şi este integrabilă şi 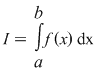 . .
Graficul functiei de gradul al II-lea
Trasarea graficului functiei de gradul doi: etape: intersectia cu axele, varful parabolei, intervale de monotonie; aplicatii.
Vezi intregul articol | Asupra unei probleme de geometrie
O problema de geometrie cu patru solutii: una sintetica, una analitica; una trigonometrica si una vectoriala. Solutia sintetica contine o constructie auxiliara; solutia trigonometrica foloseste teorema sinusurilor. Solutiile analitica si vectoriala constau in calcule directe. De remarcat ca solutiile analitica si vectoriala sunt diferite; adica solutia vectoriala nu este transpusa solutiei analitice in limbaj vectorial (si viceversa).
Vezi intregul articol | Inmultirea numerelor complexe
Inmultirea a doua numere scrise in forma algebrica: definitie, exemplu, proprietati: asociativitatea, comutativitate, existenta elementului neutru, existenta si determinarea inversului unui numar complex nenul dat, distributivitatea, aplicatii.
Vezi intregul articol | Proprietatile determinantilor - Partea II
Proprietatile determinantilor: o matrice (patratica) cu doua linii (coloane) proportionale este nul; schimband intre ele doua linii (respectiv coloane) ale unei matrice determinantul isi schimba semnul, daca doua matrice difera printr-o singura linie (sau coloana), atunci suma determinantilor acestor matrice este egala cu determinantul matricei care are pe linia respectiva (coloana respectiva) suma elementelor liniilor (sau coloanelor) respective ale celor doua matrice (restul ramânând neschimbate), determinantul produsului este egal cu produsul determinantilor, daca o linie (respectiv coloana) a unei matrice este o combinatie liniara a celorlalte linii (respectiv coloane) ale matricei, atunci determinantul matricei este nul (si reciproc), exemple.
Vezi intregul articol |
Materiale didactice
|